
【题目】已知长方形![]() ,
, ![]() ,
, ![]() .以
.以![]() 的中点
的中点![]() 为原点建立如图所示的平面直角坐标系
为原点建立如图所示的平面直角坐标系![]() .
.

(1)求以![]() 、
、![]() 为焦点,且过
为焦点,且过![]() 、
、![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 交(1)中椭圆于
交(1)中椭圆于![]() 、
、![]() 两点,是否存在直线
两点,是否存在直线![]() ,使得弦
,使得弦![]() 为直径的圆恰好过原点?若存在,求出直线
为直径的圆恰好过原点?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2 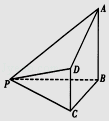
(1)证明:平面ABP⊥平面ADP;
(2)若直线PA与平面PCD所成角为α,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)(ⅰ)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ⅱ)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C1的极坐标方程为ρ=2sinθ,正方形ABCD的顶点都在C1上,且依次按逆时针方向排列,点A的极坐标为( ![]() ,
, ![]() ).
).
(1)求点C的直角坐标;
(2)若点P在曲线C2:x2+y2=4上运动,求|PB|2+|PC|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:(1)存在实数x,使![]() =
=![]() ; (2)若
; (2)若![]() 是锐角△
是锐角△![]() 的内角,则
的内角,则![]() >
>![]() ; (3)函数y=sin(
; (3)函数y=sin(![]()
![]() -
-![]() )是偶函数; (4)函数y=sin2
)是偶函数; (4)函数y=sin2![]() 的图象向右平移
的图象向右平移![]() 个单位,得到y=sin(2
个单位,得到y=sin(2![]() +
+![]() )的图象.其中正确的命题的序号是____________.
)的图象.其中正确的命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的可导函数f(x),其导函数记为f'(x),满足f(x)+f(2﹣x)=(x﹣1)2 , 且当x≤1时,恒有f'(x)+2<x.若 ![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.(﹣∞,1]
B.![]()
C.[1,+∞)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M是正四面体ABCD棱AB的中点,N是棱CD上异于端点C,D的任一点,则下列结论中,正确的个数有( )
(1)MN⊥AB;
(2)若N为中点,则MN与AD所成角为60°;
(3)平面CDM⊥平面ABN;
(4)不存在点N,使得过MN的平面与AC垂直.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥P﹣ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点, 
(1)求证:平面EBD⊥平面PAC;
(2)求直线BE与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个水轮的半径为4米,水轮圆心![]() 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点
距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点![]() 从水中浮现(图中点
从水中浮现(图中点![]() )开始计算时间.
)开始计算时间.
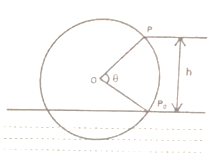
(1)将点![]() 距离水面的高度
距离水面的高度![]() (米)表示为时间
(米)表示为时间![]() (秒)的函数;
(秒)的函数;
(2)在水轮旋转一圈内,有多长时间点![]() 离开水面?
离开水面?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com