
分析 (1)由题意和二次根式的被开方数非负,可得|x+1|+|x-1|≥4,运用绝对值的意义和对x讨论,解不等式即可得到所求定义域;
(2)可得-2<a,b<2,要证2|a+b|<|4+ab|,可证4(a+b)2<(4+ab)2,作差4(a+b)2-(4+ab)2,运用平方差和因式分解,即可得证.
解答 解:(1)当m=4时,由|x+1|+|x-1|≥4,
等价于$\left\{\begin{array}{l}{x<-1}\\{-x-1-x+1≥4}\end{array}\right.$或$\left\{\begin{array}{l}{x>1}\\{x+1+x-1≥4}\end{array}\right.$或$\left\{\begin{array}{l}{-1≤x≤1}\\{x+1+1-x≥4}\end{array}\right.$,
解得x≤-2或x≥2或x∈∅.
则不等式的解集为M={x|x≤-2或x≥2};
(2)证明:当a,b∈CRM时,即-2<a,b<2,
所以4(a+b)2-(4+ab)2=4(a2+2ab+b2)-(16+8ab+a2b2)
=4a2+4b2-16-a2b2=(a2-4)(4-b2)<0,所以4(a+b)2<(4+ab)2,
即2|a+b|<|4+ab|.
点评 本题考查函数的定义域的求法,注意运用绝对值的意义,以及分类讨论的思想方法,考查不等式的证明,注意运用作差法,考查推理能力和运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
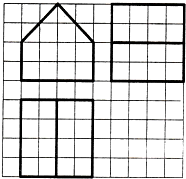 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面积为( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面积为( )| A. | $56+16\sqrt{2}$ | B. | 56+8$\sqrt{2}$ | C. | 64 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
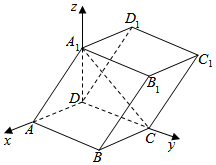 如图,在平行六面体ABCD-A1B1C1D1中,AD=1,CD=2,A1D⊥平面ABCD,AA1与底面ANCD所成角为θ(0<θ<$\frac{π}{2}$),∠ADC=2θ
如图,在平行六面体ABCD-A1B1C1D1中,AD=1,CD=2,A1D⊥平面ABCD,AA1与底面ANCD所成角为θ(0<θ<$\frac{π}{2}$),∠ADC=2θ查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知三棱锥的三视图的正视图是等腰三角形,俯视图是边长为$\sqrt{3}$的等边三角形,侧视图是等腰直角三角形,则三棱锥的四个面中面积的最大值为为$\frac{3\sqrt{6}}{4}$.
已知三棱锥的三视图的正视图是等腰三角形,俯视图是边长为$\sqrt{3}$的等边三角形,侧视图是等腰直角三角形,则三棱锥的四个面中面积的最大值为为$\frac{3\sqrt{6}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,1] | C. | (-∞,1) | D. | [-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<c<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(4x+$\frac{π}{3}$) | B. | y=sin(2x+$\frac{2π}{3}$) | C. | y=sin(2x+$\frac{π}{3}$) | D. | y=sin(4x+$\frac{2π}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com