
【题目】在边长为4的正方形ABCD的边上有动点P,动点P从B点开始沿折线BCDA运动到A终止,设P点移动的距离为x,![]() 的面积为S.
的面积为S.
(1)求函数S=f(x)的解析式、定义域,画出函数图像;
(2)求函数S=f(x)的值域. ![]()
【答案】(1)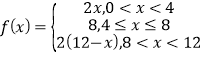 ;
;
(2)值域为![]()
【解析】
(1)分三类情况讨论,0<x≤2, 2<x≤4, 4<x≤6,分别求出S,再把S表示成分段函数的形式,进而画出函数的图象;
(2)结合图象得到函数的值域.
(1)①当点P在线段BC上运动时,点P到AB的距离为x,则y=![]() ×4×x=2x(0<x<4),其函数图象为过原点的一线段;
×4×x=2x(0<x<4),其函数图象为过原点的一线段;
②点P在边CD上时,点P到AB的距离不变,为4,则y=![]() ×4×4=8(4≤x≤8),其函数图象是平行于x轴的一线段;
×4×4=8(4≤x≤8),其函数图象是平行于x轴的一线段;
③点P在边DA上时,点P到AB的距离为(12﹣x),则y=![]() ×4×(12﹣x)=24﹣2x(8<x<12),其图象是一线段.
×4×(12﹣x)=24﹣2x(8<x<12),其图象是一线段.
∴ ,其定义域为:(0,12)
,其定义域为:(0,12)
其图象为:
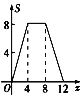
(2)结合图象可知,函数S=f(x)的值域值域为![]()


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 算得,
算得, ![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足
+y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() .
.
(1)求证: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin2x的图象,只需把函数y=sin(2x﹣ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知,利用正弦定理可得![]() a2=
a2=![]() b2+
b2+![]() c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
试题解析:
(1)因为![]() asin A=(
asin A=(![]() b-c)sin B+(
b-c)sin B+(![]() c-b)·sin C,
c-b)·sin C,
由正弦定理得![]() a2=(
a2=(![]() b-c)b+(
b-c)b+(![]() c-b)c,
c-b)c,
整理得![]() a2=
a2=![]()
![]() c2-2bc,
c2-2bc,
由余弦定理得cos A=![]() =
=![]() =
=![]() ,
,
因为A∈(0,π),所以A=![]() .
.
(2)由cos B=![]() ,得sin B=
,得sin B=![]() =
=![]() =
=![]() ,
,
所以cos C=cos[π-(A+B)]=-cos(A+B)=-![]() =-
=-![]() ,
,
由正弦定理得b=![]() =
=![]() =2,
=2,
所以CD=![]() AC=1,
AC=1,
在△BCD中,由余弦定理得BD2=(![]() )2+12-2×1×
)2+12-2×1×![]() ×
×![]() =13,
=13,
所以BD=![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 给出下列四个命题:
给出下列四个命题:
①c = 0时,![]() 是奇函数; ②
是奇函数; ②![]() 时,方程
时,方程![]() 只有一个实根;
只有一个实根;
③![]() 的图象关于点(0 , c)对称; ④方程
的图象关于点(0 , c)对称; ④方程![]() 至多3个实根.
至多3个实根.
其中正确的命题个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
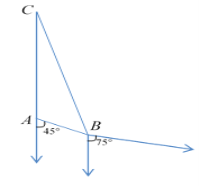
【题目】如图,在海岸A处,发现南偏东45°方向距A为(2![]() -2)海里的B处有一艘走私船,在A处正北方向,距A为
-2)海里的B处有一艘走私船,在A处正北方向,距A为![]() 海里的C处的缉私船立即奉命以10
海里的C处的缉私船立即奉命以10![]() 海里/时的速度追截走私船.
海里/时的速度追截走私船.
(1)刚发现走私船时,求两船的距离;
(2)若走私船正以10![]() 海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:
海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:![]() ≈1.4,
≈1.4,![]() ≈2.5).
≈2.5).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com