
【题目】已知函数![]() .
.
(1)求![]() 的图像在点
的图像在点![]() 处的切线方程;
处的切线方程;
(2)求![]() 在区间
在区间![]() 上的取值范围.
上的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先求出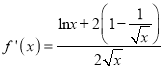 ,再求出
,再求出![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)利用导数研究函数的单调性可得当
处的切线方程;(2)利用导数研究函数的单调性可得当![]() 时,
时, ![]() 递增;当
递增;当![]() 时
时![]() 递减;可得所以
递减;可得所以![]() ,
, ![]() .
.
试题解析:(1)![]() ,
, ![]()
所以![]()
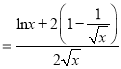
则![]() .又
.又![]() ,所以
,所以![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)由(1)知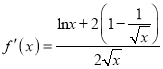 .
.
因为![]() 与
与![]() 都是区间
都是区间![]() 上的增函数,所以
上的增函数,所以![]() 是
是![]() 上的增函数.
上的增函数.
又![]() ,所以当
,所以当![]() 时,
时, ![]() ,即
,即![]() ,此时
,此时![]() 递增;
递增;
当![]() 时
时![]() ,即
,即![]() ,此时
,此时![]() 递减;
递减;
又![]() ,
, 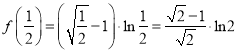 ,
, ![]() .
.
所以![]() ,
, ![]() .
.
所以![]() 在区间
在区间![]() 的取值范围为
的取值范围为![]()
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与最值,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),过原点的两条直线
为参数),过原点的两条直线![]() 分别与曲线
分别与曲线![]() 交于异于原点的
交于异于原点的![]() 、
、![]() 两点,且
两点,且![]() ,其中
,其中![]() 的倾斜角为
的倾斜角为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动规定,一次购物付款总额:
(1)如果标价总额不超过200元,则不给予优惠;
(2)如果标价总额超过200元但不超过500元,则按标价总额给予9折优惠;
(3)如果标价总额超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予8折优惠.
某人两次去购物,分别付款180元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.550元B.560元C.570元D.580元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的数学学习能力,进行了主题分别为“运算”、“推理”、“想象”、“建模”四场竞赛.规定:每场竞赛前三名得分分别为![]() 、
、![]() 、
、![]() (
(![]() ,且
,且![]() 、
、![]() 、
、![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终得分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终得分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“运算”这场竞赛中获得了第一名,那么“运算”这场竞赛的第三名是( )
分,且乙在“运算”这场竞赛中获得了第一名,那么“运算”这场竞赛的第三名是( )
A.甲B.乙C.丙D.甲和丙都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,乙校教师记为
,乙校教师记为![]() ,丙校教师记为
,丙校教师记为![]() ,丁校教师记为
,丁校教师记为![]() .现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
(3)求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆的一个顶点与两个焦点构成的三角形面积为2.
,椭圆的一个顶点与两个焦点构成的三角形面积为2.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与
两点,且与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点.
两点.
(i)若![]() ,求
,求![]() 的值;
的值;
(ii)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com