练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知已知圆 经过 、 两点，且圆心C在直线 上，求解：（1）圆C的方程；（2）若直线 与圆 总有公共点，求实数 的取值范围.
    （1）求圆C的方程；
    （2）若直线 与圆 总有公共点，求实数 的取值范围.

    【答案】
    （1）

    由于AB的中点为 ， ，则线段AB的垂直平分线方程为 ， 而圆心C是直线 与直线 的交点，由 解得 ，即圆心 ，又半径为 ，故圆C的方程为 ；


    （2）

    圆心 到直线 的距离 得 ，解得 .


    【解析】分析：本题主要考查了直线与圆的位置关系，解决问题的关键是(1)通过AB的中点为 ， ，得到AB的垂直平分线方程为 ， 因为圆心C是直线 与直线 的交点，联立得到圆心 ，根据 ，得到圆C的方程为；(2)根据直线与圆相交圆心到直线的距离小于半径计算即可.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某投资公司现提供两种一年期投资理财方案，一年后投资盈亏的情况如下表：

    投资股市

    获利

    不赔不赚

    亏损

    购买基金

    获利

    不赔不赚

    亏损

    概率

    概率

    （Ⅰ）甲、乙两人在投资顾问的建议下分别选择“投资股市”和“买基金”，若一年后他们中至少有一人盈利的概率大于，求的取值范围；

    （Ⅱ）若，某人现有万元资金，决定在“投资股市”和“购买基金”这两种方案中选择出一种，那么选择何种方案可使得一年后的投资收益的数学期望值较大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，台风中心从A地以每小时20千米的速度向东北方向（北偏东）移动，离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系，解决以下问题：

    (1) 求台风移动路径所在的直线方程;

    (2)求城市B处于危险区域的时间是多少小时？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （Ⅰ）当时，求的最大值；

    （Ⅱ）若对恒成立，求的取值范围；

    （Ⅲ）证明

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax+ （ab≠0）．
    （1）当b=a=1时，求函数f（x）的单调区间；
    （2）若函数f（x）在点（2，f（2））处的切线方程是y=2x﹣3，证明：曲线y=f（x）上任一点处的切线与直线x=1和直线y=x所围成的三角形面积为定值，并求出此定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 和 是平面内互相垂直的两条直线，它们的交点为A，异于点A的两动点B、C分别在 、 上，且BC= ，则过A、B、C三点圆的面积为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）= 是奇函数，则使f（x）＞4成立的x的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：sinθ=ρcos2θ，过点M（﹣1，2）的直线l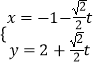： （t为参数）与曲线C相交于A、B两点．求：
    （1）线段AB的长度；
    （2）点M（﹣1，2）到A、B两点的距离之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个棱锥的侧棱长都相等，那么这个棱锥（ ）
    A.一定是正棱锥
    B.一定不是正棱锥
    C.是底面为圆内接多边形的棱锥
    D.是底面为圆外切多边形的棱锥

    查看答案和解析>>

    同步练习册答案