
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,….
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出严格的证明.
(1) a1=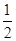 . a2=
. a2=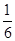
(2)猜想Sn=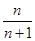 ,n=1,2,3,….
,n=1,2,3,….
【解析】(1)先令n=1,则s1-1即a1-1是方程的一个根,因而建立关于a1的方程求出a1的值.同理再利用n=2时,求出a2.
(2)由条件可知(Sn-1)2-an(Sn-1)-an=0,化简得S-2Sn+1-anSn=0,
然后利用n≥2时,an=Sn-Sn-1,把an代入上式,消去an,就找到了sn与sn-1之间的递推关系,求出s1,s2,s3,然后观察规律,归纳出sn,再利用数学归纳法证明即可
(1)当n=1时,x2-a1x-a1=0有一根为S1-1=a1-1,于是(a1-1)2-a1(a1-1)-a1=0,解得a1=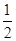 . 当n=2时,x2-a2x-a2=0有一根为S2-1=a2-
. 当n=2时,x2-a2x-a2=0有一根为S2-1=a2-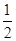 ,
于是(a2-
,
于是(a2-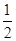 )2-a2(a2-
)2-a2(a2-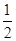 )-a2=0,解得a2=
)-a2=0,解得a2=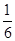
(2)由题设(Sn-1)2-an(Sn-1)-an=0,S-2Sn+1-anSn=0.当n≥2时,an=Sn-Sn-1,
代入上式得Sn-1Sn-2Sn+1=0.①由(1)得S1=a1=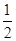 ,S2=a1+a2=
,S2=a1+a2=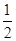 +
+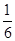 =
= .
.
由①可得S3=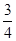 .由此猜想Sn=
.由此猜想Sn=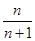 ,n=1,2,3,….
,n=1,2,3,….
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即Sk=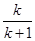 ,当n=k+1时,由①得Sk+1=
,当n=k+1时,由①得Sk+1=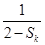 ,即Sk+1=
,即Sk+1=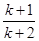 ,故n=k+1时结论也成立.
,故n=k+1时结论也成立.
综上,由(i)、(ii)可知Sn=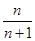 对所有正整数n都成立.
对所有正整数n都成立.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 10 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| Sn |
| 5•2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com