
【题目】已知函数![]() .
.
(I)若![]() ,判断
,判断![]() 上的单调性;
上的单调性;
(Ⅱ)求函数![]() 上的最小值;
上的最小值;
(III)当![]() 时,是否存在正整数n,使
时,是否存在正整数n,使![]() 恒成立?若存在,求出n的最大值;若不存在,说明理由.
恒成立?若存在,求出n的最大值;若不存在,说明理由.
【答案】(I)见解析;(Ⅱ)见解析; (III)见解析
【解析】
(I)根据f′(x)的符号得出结论;
(II)讨论a的范围,得出f(x)在[1,e]上单调性,根据单调性得出最小值;
(III)化简不等式可得n+xlnx![]() ,根据两侧函数的单调性得出两函数在极值点处的函数值的大小,从而得出n的范围.
,根据两侧函数的单调性得出两函数在极值点处的函数值的大小,从而得出n的范围.
(Ⅰ)当![]() 时,
时,![]()
由于![]() ,故
,故![]() ,
,
![]() 在
在![]() 单调递增.
单调递增.
(Ⅱ)![]()
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
当![]() 时,由
时,由![]() 解得
解得![]() (负值舍去)
(负值舍去)
设![]()
若![]() ,即
,即![]() ,也就是
,也就是![]() 时,
时,![]() 单调递增,
单调递增,
![]() ,
,
若![]() ,即
,即![]() 时
时
![]() 单调递减,
单调递减,
![]() 单调递增.
单调递增.
故![]()
若![]() 即
即![]() 时
时![]() 单调递减
单调递减
![]() ,
,
综上所述:当![]() 时,
时,![]() 的最小值为1;
的最小值为1;
当![]() 时,
时,![]() 的最小值为
的最小值为![]()
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(Ⅲ)当![]() 时,不等式为
时,不等式为![]()
![]() 恒成立
恒成立
由于![]() ,故
,故![]() 成立,
成立,![]() ,又
,又![]()
所以n只可能为1或2.
下证![]() 时不等式
时不等式![]() 恒成立
恒成立
事实上,设![]()
![]() ,
,
又设![]() 在
在![]() 单调递增
单调递增
故![]()
即![]()
所以当![]() 时,
时,![]() 单调递减,
单调递减,
![]() 时,
时,![]() 单调递增,
单调递增,
故![]()
即![]() 时,
时,![]() ,对
,对![]() 恒成立,
恒成立,
所以存在正整数n,且n的最大值为2,满足题意.


科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中装有形状、大小都相同的6只小球,其中有3只红球、2只黄球和1只蓝球.若从中1次随机摸出2只球,则1只红球和1只黄球的概率为__________,2只球颜色相同的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”.现提供4种颜色给“弦图”的5个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
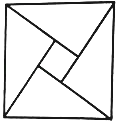
A.48种B.72种C.96种D.144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的长轴长与焦距之比为
的长轴长与焦距之比为![]() ,过
,过![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
(2)若在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 是以
是以![]() 为顶点的等腰三角形,求直线
为顶点的等腰三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com