
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)证明![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(2)求![]() ;
;
(3)设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.

(1)求椭圆C的方程;
(2)椭圆C上是否存在点P,使得过点P引圆O:x2+y2=b2的两条切线PA、PB互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业一天中不同时刻的用电量![]() (万千瓦时)关于时间
(万千瓦时)关于时间![]() (单位:小时,其中
(单位:小时,其中![]() 对应凌晨0点)的函数
对应凌晨0点)的函数![]() 近似满足
近似满足![]()
![]() ,如图是函数
,如图是函数![]() 的部分图象.
的部分图象.

(1)求![]() 的解析式;
的解析式;
(2)已知该企业某天前半日能分配到的供电量![]() (万千瓦时)与时间
(万千瓦时)与时间![]() (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型![]() 模拟,当供电量
模拟,当供电量![]() 小于企业用电量
小于企业用电量![]() 时,企业必须停产.初步预计开始停产的临界时间
时,企业必须停产.初步预计开始停产的临界时间![]() 在中午11点到12点之间,用二分法估算
在中午11点到12点之间,用二分法估算![]() 所在的一个区间(区间长度精确到15分钟).
所在的一个区间(区间长度精确到15分钟).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的三角形ABC中,一机器人从三角形ABC上的每一个顶点移动到另一个顶点,(规定:每次只能从一个顶点移动到另一个顶点),而且按逆时针方向移动的概率为顺时针方向移动的概率的3倍,假设现在机器人的初始位置为顶点A处,则通过三次移动后返回到A处的概率为________________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解居民喜欢中华传统文化是否与年龄有关,随机调查了60位居民,相关数据统计如下表所示,
喜欢 | 不喜欢 | 合计 | |
大于45岁 | 26 | 6 | 32 |
25岁至45岁 | 13 | 15 | 28 |
合计 | 39 | 21 | 60 |
(Ⅰ)是否有99.5%以上的人把握认为喜欢中华传统文化与年龄有关?
(Ⅱ)按年龄采用分层抽样的方法从喜欢中华传统文化的受调查居民中随机抽取6人作进一步了解,若从这6位居民中任选2人,求这2人的年龄均大于45岁的概率.
附:![]()
![]()
| 0.025 | 0.010 | 0.005 | 0,001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
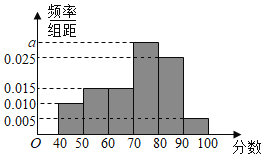
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的序号是____________。
①数列{an}的前n项和![]() ,则数列{ an }是等差数列。
,则数列{ an }是等差数列。
②若等差数列{ an }中,已知![]()
![]()
![]() ,则
,则![]()
![]()
③函数![]() 的最小值为2。
的最小值为2。
④等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() 最大时
最大时![]() 13
13
⑤若数列{an}是等比数列,其前n项和为![]() 则常数k的值为1.
则常数k的值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,原文是:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之. 翻译为现代的语言如下:如果需要对分数进行约分,那么可以折半的话,就折半(也就是用2来约分).如果不可以折半的话,那么就比较分母和分子的大小,用大数减去小数,互相减来减去,一直到减数与差相等为止,用这个相等的数字来约分,现给出“更相减损术”的程序框图如图所示,如果输入的![]() ,
,![]() ,则输出的
,则输出的![]() ( )
( )

A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c)(a﹣b+c)=ac.
(1)求B.
(2)若sinAsinC= ![]() ,求C.
,求C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com