
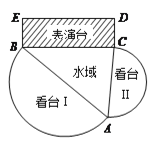
【题目】在一水域上建一个演艺广场.演艺广场由看台Ⅰ,看台Ⅱ,三角形水域![]() ,及矩形表演台
,及矩形表演台![]() 四个部分构成(如图).看台Ⅰ,看台Ⅱ是分别以
四个部分构成(如图).看台Ⅰ,看台Ⅱ是分别以![]() ,
, ![]() 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍;矩形表演台
为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍;矩形表演台![]() 中,
中, ![]() 米;三角形水域
米;三角形水域![]() 的面积为
的面积为![]() 平方米.设
平方米.设![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的长;
的长;
(Ⅱ)若表演台每平方米的造价为![]() 万元,求表演台的最低造价.
万元,求表演台的最低造价.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】某中学高三文科班学生参加了数学与地理水平测试,学校从测试合格的学生中随机抽取100人的成绩进行统计分析.抽取的100人的数学与地理的水平测试成绩如下表:

成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(2)若样本中![]() ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a为常数)有两个极值点.
(a为常数)有两个极值点.
(1)求实数a的取值范围;
(2)设f(x)的两个极值点分别为x1,x2,若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
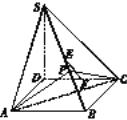
【题目】四棱锥S-ABCD中的底面是菱形,∠BAD=60°,SD⊥底面ABCD,SD=AB=2,E、F分别为SB、CD的中点.
(Ⅰ)求证:EF∥平面SAD;
(Ⅱ)点P是SB上一点,若SB⊥平面APC,试确定点P的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)选修4-2:矩阵与变换
求矩阵![]() 的特征值和特征向量.
的特征值和特征向量.
(2)选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的方程为
的方程为![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆![]() 的参数方程
的参数方程![]() (
(![]() 是参数),若圆
是参数),若圆![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856306)
在△ABC中,内角A,B,C的对边分别为a,b,c,已知![]() ,且b=5,acos C=-1.
,且b=5,acos C=-1.
(Ⅰ)求角A;
(Ⅱ)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
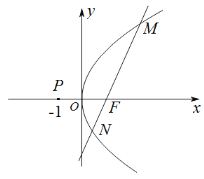
【题目】已知点![]() 为抛物线C:
为抛物线C:![]() 的焦点,过点
的焦点,过点![]() 的动直线
的动直线![]() 与抛物线C交于
与抛物线C交于![]() ,
,![]() 两点,如图.当直线
两点,如图.当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求抛物线C的方程;
(2)已知点![]() ,设直线PM的斜率为
,设直线PM的斜率为![]() ,直线PN的斜率为
,直线PN的斜率为![]() .请判断
.请判断![]() 是否为定值,若是,写出这个定值,并证明你的结论;若不是,说明理由.
是否为定值,若是,写出这个定值,并证明你的结论;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com