
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上存在单调增区间,求实数
上存在单调增区间,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,证明:对于
,证明:对于![]() ,总有
,总有![]()
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)求出![]() 的导数,将其转化为在区间
的导数,将其转化为在区间![]() 内存在区间使得即
内存在区间使得即![]() 在
在![]() 上能成立,根据函数
上能成立,根据函数![]() 的最小值即可确定
的最小值即可确定![]() 的范围;(2)问题转化为证明
的范围;(2)问题转化为证明![]() ,在
,在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,
,![]() ,求出
,求出![]() 的导数,判断出函数的单调性,从而证出结论.
的导数,判断出函数的单调性,从而证出结论.
(1)由题![]() ,
,
因为函数![]() 在
在![]() 存在单调增区间,
存在单调增区间,
故在区间![]() 内存在区间使得
内存在区间使得![]() 成立,
成立,
即![]() 能成立,
能成立,
即![]() 在
在![]() 上能成立,
上能成立,
而![]() 在
在![]() 的最小值是
的最小值是![]() ,
,
故![]() ;
;
(2)若![]() ,则
,则![]() ,
,
![]() ,
,
而![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
要证原不等式成立,只要证![]() ,
,
只要证![]() ,
,
只要证![]() ,在
,在![]() 上恒成立,
上恒成立,
首先构造函数![]() ,
,![]() ,
,
因为 ,
,
可得,在![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是减函数,
上是减函数,
在![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是增函数,
上是增函数,
所以,在![]() 上,
上,![]() ,所以
,所以![]() ,
,
所以,![]() ,等号成立当且仅当
,等号成立当且仅当![]() 时,
时,
其次构造函数![]() ,
,![]() ,
,
因为![]() ,
,
可见![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是减函数,
上是减函数,
![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是增函数,
上是增函数,
所以在![]() 上,
上,![]() ,所以
,所以![]() ,
,
所以,![]() ,等号成立当且仅当
,等号成立当且仅当![]()
![]() 时.
时.
综上所述,![]() ,
,
因为取等条件并不一致,
所以![]() ,在
,在![]() 上恒成立,
上恒成立,
所以![]() ,总有
,总有![]() 成立.
成立.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
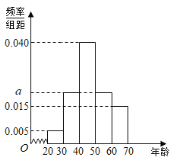
(1)求图中的a值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中,各抽取多少人;
(3)由频率分布直方图,求所有被调查人员的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若不等式![]() 的解集为
的解集为![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)![]() 时,
时,
①当![]() 时,若不等式
时,若不等式![]() 在
在![]() 有解,求
有解,求![]() 的取值范围;
的取值范围;
②当![]() 时,设
时,设![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且满足![]() (k∈R).
(k∈R).
(1)求k和数列{an}的通项公式;
(2)若数列{bn}满足bn=![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,
,![]() 为坐标原点,
为坐标原点,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() 、
、![]() ,且
,且![]() ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求![]() 的最大值,若不存在说明理由.
的最大值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取的礼物都满意,那么不同的选法有( )
A. 50种B. 60种C. 70种D. 90种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年前5个月某种产品的产量(单位:万件)的数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 4 | 6 | 6 |
(1)若从这5组数据中随机抽出2组,求抽出的2组数据恰好是不相邻两个月的数据的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计今年6月份该种产品的产量.
,并估计今年6月份该种产品的产量.
参考公式: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com