
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
![]()
已知![]() 和
和![]() 具有线性相关关系
具有线性相关关系
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润![]() 取到最大值?(保留一位小数)
取到最大值?(保留一位小数)
参考数据及公式: ![]() ,
, ![]()

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系xoy中,直线l的参数方程是 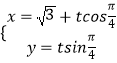 (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x)的图象关于点 ![]() 成中心对称,对任意的实数x都有f(x)=﹣f(x+
成中心对称,对任意的实数x都有f(x)=﹣f(x+ ![]() ),且f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+f(3)+…+f(2014)的值为( )
),且f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+f(3)+…+f(2014)的值为( )
A.2
B.1
C.﹣1
D.﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=4x2-2(t-2)x-2t2-t+1在区间[-1,1]内至少存在一个值m,使得f(m)>0,则实数t的取值范围( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣|x|+2a﹣1(a为实常数).
(1)若a=1,求f(x)=3的解;
(2)求f(x)在区间[1,2]的最小值为g(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为R,且满足
(1)f(1)=3
(2)对于任意的![]() ,总有
,总有![]()
(3)对于任意的![]()
(I)求f(0)及f(-1)的值
(II)求证:函数y=f(x)-1为奇函数
(III)若![]() ,求实数m的取值范围
,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com