【答案】
分析:由三角形的三边的大小,根据大边对大角可得AC所对的角为最大角,即B为三角形的最大角,利用余弦定理表示出cosB,把已知的三边长代入求出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数,即为三角形最大角的度数.
解答:解:∵AB=c=4,BC=a=3,AC=b=

,
∴b>c>a,即b为最大边,
∴B为最大角,
由余弦定理得:cosB=

=

=-

,
又B∈(0,180°),
∴B=120°,
则△ABC的最大角的大小为120°.
故答案为:120°
点评:此题考查了余弦定理,三角形的边角关系,以及特殊角的三角函数值,余弦定理很好的建立了三角形的边角关系,熟练掌握余弦定理是解本题的关键.

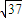 ,则△ABC的最大角的大小为 .
,则△ABC的最大角的大小为 .  ,
, =
= =-
=- ,
,
