练习册

  • 练习册
  • 试题
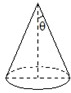    精英家教网 > 高中数学 > 题目详情
    如图所示，已知圆锥的底面半径为R，高为H，在其中有一个高为x，下底面半径与上底面半径之比为λ(0<λ<1)的内接圆台．试问：当x为何值时，圆台的体积最大?并求出这个最大的体积．

    答案：
    解析：

    		设内接圆台的上底面半径为r，则下底面半径为λr．由相似三角形的性质，得r=R(1－)．从而圆台的体积为

    =

    =                   

    =．

    由

    又为定值．

    ∴当时，V最大．

    故当时，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网已知圆锥的底面半径为5cm，侧面积为65πcm2，设圆锥的母线与高的夹角为θ（如图所示），则sinθ的值为（　　）
    A、
    5
    12
    B、
    5
    13
    C、
    10
    13
    D、
    12
    13

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•延安模拟）如右图所示，已知0为矩形ABCD的边CD上一点，以直线CD为旋转轴，旋转这个矩形所得的几何体体积为1，其中以OA为母线的圆锥体积为
    1
    4
    ，则以OB为母线的圆锥体积为
    1
    12
    1
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    如图所示，已知圆锥的底面半径为R，高为H，在其中有一个高为x，下底面半径与上底面半径之比为λ(0<λ<1)的内接圆台．试问：当x为何值时，圆台的体积最大?并求出这个最大的体积．

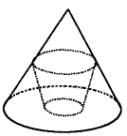
    查看答案和解析>>

    科目：高中数学 来源：2015届福建省高一下学期第一次月考数学试卷（解析版） 题型：解答题

    如图所示，已知在圆锥SO中，底面半径r＝1，母线长l＝4，M为母线SA上的一个点，且SM＝x，从点M拉一根绳子，围绕圆锥侧面转到点A，求：

    (1)设f(x)为绳子最短长度的平方，求f(x)表达式；

    (2)绳子最短时，顶点到绳子的最短距离；

    (3)f(x)的最大值．

     

    查看答案和解析>>

    同步练习册答案