
【题目】如图①,已知矩形ABCD满足AB=5,![]() ,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱
,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱![]() .
.
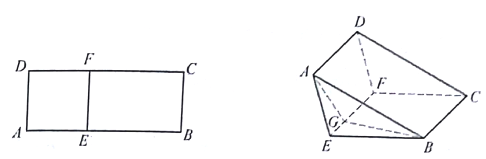
⑴若图②中△ABG是直角三角形,这里G是线段EF上的点,试求线段EG的长度x的取值范围;
⑵若⑴中EG的长度为取值范围内的最大整数,且线段AB的长度取得最小值,求二面角![]() 的值;
的值;
⑶在⑴与⑵的条件都满足的情况下,求三棱锥A-BFG的体积.
科目:高中数学 来源: 题型:
【题目】甲、乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的5道题。规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中的5道题。规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(I)求甲能入选的概率.
(II)求乙得分的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,E,F分别为AC,BC的中点.
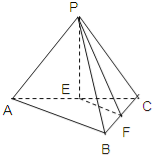
(1)求证:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A 为椭圆![]() 的下顶点,过 A 的直线 l 交抛物线
的下顶点,过 A 的直线 l 交抛物线![]() 于B、C 两点,C 是 AB 的中点.
于B、C 两点,C 是 AB 的中点.
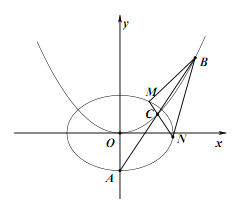
(I)求证:点C的纵坐标是定值;
(II)过点C作与直线 l 倾斜角互补的直线l交椭圆于M、N两点,求p的值,使得△BMN的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若函数在区间![]() 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围;
(2)问是否存在常数![]() ,使得当
,使得当![]() 时,
时,![]() 的值域为区间D,且D的长度为
的值域为区间D,且D的长度为![]() .
.
(注:区间![]()
![]() 的长度为
的长度为![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上的点到焦点的最长距离为
,且椭圆上的点到焦点的最长距离为![]() .
.
(1)求椭圆C的方程;
(2)过点P(0,2)的直线l(不过原点O)与椭圆C交于两点A、B,M为线段AB的中点.
(ⅰ)证明:直线OM与l的斜率乘积为定值;
(ⅱ)求△OAB面积的最大值及此时l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年,大连“蜗享出行”正式引领共享汽车,改变人们传统的出行理念,给市民出行带来了诸多便利![]() 该公司购买了一批汽车投放到市场给市民使用
该公司购买了一批汽车投放到市场给市民使用![]() 据市场分析,每辆汽车的营运累计收入
据市场分析,每辆汽车的营运累计收入![]() 单位:元
单位:元![]() 与营运天数
与营运天数![]() 满足
满足![]() .
.
![]() 要使营运累计收入高于1400元求营运天数的取值范围;
要使营运累计收入高于1400元求营运天数的取值范围;
![]() 每辆汽车营运多少天时,才能使每天的平均营运收入最大?
每辆汽车营运多少天时,才能使每天的平均营运收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点到短轴的端点的距离为
的焦点到短轴的端点的距离为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com