
【题目】已知m,n∈R+,f(x)=|x+m|+|2x-n|.
(1)当m=n=1时,求f(x)的最小值;
(2)若f(x)的最小值为2,求证![]() .
.
【答案】(1) ![]() . (2)见解析.
. (2)见解析.
【解析】试题分析:(1)代入m=n=1,却掉绝对值,得到分段函数,判定分段函数的单调性,确定函数的最小值;
(2)由题意得,函数的最小值为2,得![]() ,利用基本不等式求解最值,即可证明.
,利用基本不等式求解最值,即可证明.
试题解析:
(1)∵f(x)=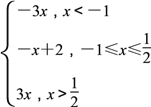
∴f(x)在(-∞,![]() )是减函数,在(
)是减函数,在(![]() ,+∞)是增函数,∴当x=
,+∞)是增函数,∴当x=![]() 时,f(x)取最小值
时,f(x)取最小值![]() .
.
(2)∵f(x)=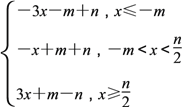 ,
,
∴f(x)在(-∞,![]() )是减函数,在(
)是减函数,在(![]() ,+∞)是增函数,
,+∞)是增函数,
∴当x=![]() 时,f(x)取最小值f(
时,f(x)取最小值f(![]() )=m+
)=m+![]() .
.
∵m,n∈R,∴![]() +
+![]() =
=![]() (
(![]() +
+![]() )(m+
)(m+![]() )
)
=![]() (2+
(2+![]() +
+![]() )≥2
)≥2
点晴:本题主要考查了绝含有绝对值的函数的最小值问题及分段函数的图象与性质、基本不等式的应用,属于中档试题,着重考查了分类讨论思想与转化与化归思想的应用,本题的解答中,根据绝对值的概念合理去掉绝对值号,转化为分段函数,利用分段函数的图象与性质,确定函数的最小值,构造基本不等式的条件,利用基本不等式是解答问题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线为
轴垂直的直线为![]() ,
, ![]() 轴,交
轴,交![]() 于点
于点![]() ,直线
,直线![]() 垂直平分
垂直平分![]() ,交
,交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,且
,且![]() (
(![]() 为常数),直线
为常数),直线![]() 与
与![]() 平行,且与曲线
平行,且与曲线![]() 相切,切点为
相切,切点为![]() ,试问
,试问![]() 的面积是否为定值.若为定值,求出
的面积是否为定值.若为定值,求出![]() 的面积;若不是定值,说明理由.
的面积;若不是定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
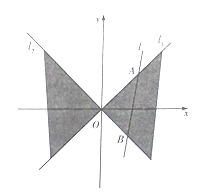
【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分即为
之间的阴影部分即为![]() ,区域
,区域![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)动直线![]() 穿过区域
穿过区域![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与轨迹
与轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证: ![]() 的面积恒为定值.
的面积恒为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}(n∈N*),首项a1=3,前n项和为Sn,且S3+a3、S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)数列{nan}的前n项和为Tn,若对任意正整数n,都有Tn∈[a,b],求b-a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=![]() x上时,求直线AB的方程.
x上时,求直线AB的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2![]() ,AB=1,AC=2,∠BAC=60°,则球O的表面积为
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
A. 4![]() B. 12
B. 12![]() C. 16
C. 16![]() D. 64
D. 64![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中, ![]() ,动点
,动点![]() 满足:以
满足:以![]() 为直径的圆与
为直径的圆与![]() 轴相切.
轴相切.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 两点,当
两点,当![]() 与
与![]() 的面积之和取得最小值时,求直线
的面积之和取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com