
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)![]() ,
,![]() 恒成立,求最大的正整数
恒成立,求最大的正整数![]() 的值;
的值;
(3)![]() ,
,![]() 且
且![]() ,证明:
,证明:![]() .
.
【答案】(1)单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(2)8;(3)证明见解析.
;(2)8;(3)证明见解析.
【解析】
(1)![]() 时,函数
时,函数![]() ,求导可得
,求导可得![]() ,可知函数
,可知函数![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,即可得出单调区间;
,即可得出单调区间;
(2)![]() ,
,![]() 恒成立,即
恒成立,即![]() ,化为
,化为![]() 很成立,利用导数研究函数的单调性求得
很成立,利用导数研究函数的单调性求得![]() 的最小值即可求解.
的最小值即可求解.
(3)![]() ,
,![]() 且
且![]() ,要证明:
,要证明:![]() .
.
![]() ,
,![]() ,
,
即![]() ,
,
令![]() ,即证明
,即证明![]() 时,
时,![]() 恒成立;
恒成立;![]() 时,
时,![]() 恒成立,利用导数研究
恒成立,利用导数研究![]() 单调性,进而证明即可.
单调性,进而证明即可.
(1)解:![]() 时,函数
时,函数![]() ,
,
则![]() ,
,
因为函数![]() 在
在![]() 上单调递增,
上单调递增,
且![]() ,∴
,∴![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
∴函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)解:因为![]() ,
,![]() 恒成立,
恒成立,
即![]() 恒成立,则
恒成立,则![]() 恒成立.
恒成立.
因为![]() ,
,
令![]() ,所以
,所以![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以当![]() 时,函数
时,函数![]() 取得极小值即最小值,
取得极小值即最小值,
因为![]() ,
,
所以![]() ,
,
所以![]() 的最大正整数值为8.
的最大正整数值为8.
(3)证明:![]() ,
,![]() 且
且![]() ,
,
要证明![]() ,
,
只需证![]() ,
,![]() .
.
即证![]() ,
,
设![]() ,
,
则![]() 时,
时,![]() 恒成立;
恒成立;![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,
,
![]() ,
,
因为函数![]() 在
在![]() 内单调递增,且
内单调递增,且![]() ,∴
,∴![]() ,
,
所以![]() 在
在![]() 时单调递减,
时单调递减,
所以![]() ,
,
所以![]() 在
在![]() 内单调递增,
内单调递增,
所以![]() ,成立;
,成立;
同理可得![]() 时,
时,![]() 恒成立,
恒成立,
综上可得,![]() ,
,![]() 且
且![]() ,
,
![]()


科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 的三内角A,B,C的对边,其面积
的三内角A,B,C的对边,其面积![]() ,在等差数列
,在等差数列![]() 中,
中,![]() ,公差
,公差![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:

(1)在给定的坐标系中画出表中数据的散点图,并由散点图判断销售件数![]() 与进店人数
与进店人数![]() 是否线性相关?(给出判断即可,不必说明理由)
是否线性相关?(给出判断即可,不必说明理由)
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测进店人数为80时,商品销售的件数(结果保留整数).
的回归方程(系数精确到0.01),预测进店人数为80时,商品销售的件数(结果保留整数).
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:回归方程![]() ,其中
,其中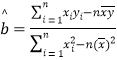 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
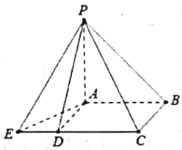
【题目】中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,若鳖臑
,若鳖臑![]() 的外接球的体积为
的外接球的体积为![]() ,则阳马
,则阳马![]() 的外接球的表面积等于______。
的外接球的表面积等于______。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com