
【题目】一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+ax+a)e﹣x , (a为常数,e为自然对数的底).
(1)当a=0时,求f′(2);
(2)若f(x)在x=0时取得极小值,试确定a的取值范围;
(3)在(2)的条件下,设由f(x)的极大值构成的函数为g(a),将a换元为x,试判断曲线y=g(x)是否能与直线3x﹣2y+m=0(m为确定的常数)相切,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
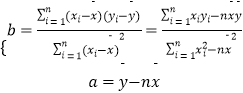
(1)画出散点图;
(2)求线性回归方程;
(3)预测当广告费支出为7百万元时的销售额.参考公式:.
查看答案和解析>>
科目:高中数学 来源: 题型:
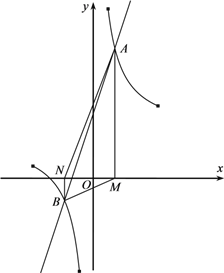
【题目】如图,已知直线![]() 与曲线
与曲线![]() 在第一象限和第三象限分别交于点
在第一象限和第三象限分别交于点![]() 和点
和点![]() ,分别由点
,分别由点![]() 、
、![]() 向
向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]() 、
、![]() ,记四边形
,记四边形![]() 的面积为S.
的面积为S.
⑴ 求出点![]() 、
、![]() 的坐标及实数
的坐标及实数![]() 的取值范围;
的取值范围;
⑵ 当![]() 取何值时,S取得最小值,并求出S的最小值.
取何值时,S取得最小值,并求出S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
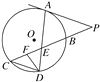
【题目】如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD,BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:∠P=∠EDF;
(2)求证:CE·EB=EF·EP;
(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin2x+2 ![]() cos2x﹣
cos2x﹣ ![]() ,函数g(x)=mcos(2x﹣
,函数g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若存在x1 , x2∈[0,
)﹣2m+3(m>0),若存在x1 , x2∈[0, ![]() ],使得f(x1)=g(x2)成立,则实数m的取值范围是( )
],使得f(x1)=g(x2)成立,则实数m的取值范围是( )
A.(0,1]
B.[1,2]
C.[ ![]() ,2]
,2]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
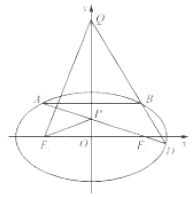
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点
,且椭圆上一点![]() 与椭圆左右两个焦点构成的三角形周长为
与椭圆左右两个焦点构成的三角形周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,设点![]() 为椭圆上任意一点,直线
为椭圆上任意一点,直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,求证:
两点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ) ![]() 的最小正周期为π,
的最小正周期为π,
(1)求当f(x)为偶函数时φ的值;
(2)若f(x)的图象过点( ![]() ,
, ![]() ),求f(x)的单调递增区间.
),求f(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com