
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() (
(![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列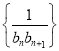 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1) 由![]() 可得
可得![]() ,两式相减得,
,两式相减得, ![]() ,即
,即![]() (
(![]() ,
, ![]() ),从而可得数列
),从而可得数列![]() 为等比数列,进而可得数列
为等比数列,进而可得数列![]() 的通项公式;(2)由(1)得,
的通项公式;(2)由(1)得, ![]() ,
, ![]() ,利用裂项相消法求解即可.
,利用裂项相消法求解即可.
试题解析:(1) ![]() ,
,
由![]() ①,可得
①,可得![]() ②.
②.
①-②得, ![]() ,即
,即![]() (
(![]() ,
, ![]() ).
).
故![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() .
.
(1)由(1)得, ![]() ,
,
所以![]() .
.
所以![]() .
.
【方法点晴】本题主要考查等比数列的定义与通项公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
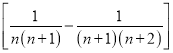 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 ![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求E的方程;
(Ⅱ)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则函数f(x)的定义域为( )
A.[0,+∞]
B.(0,1)
C.[﹣9,+∞)
D.[﹣9,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设公差不为零的等差数列{an}的前5项的和为55,且a2 , ![]() ﹣9成等比数列.
﹣9成等比数列.
(1)求数列{an}的通项公式.
(2)设数列bn= ![]() ,求证:数列{bn}的前n项和Sn<
,求证:数列{bn}的前n项和Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N*
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0,C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有 ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
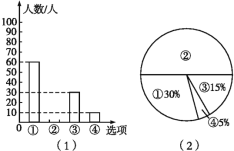
(1)本次一共调查了多少名学生.(2)在图(1)中将②对应的部分补充完整.
(3)若该校有3 000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5时以下?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人单独购买A,B商品分别付款168元和423元,假设他一次性购买A,B两件商品,则应付款是
A. 413.7元 B. 513.7元 C. 546.6元 D. 548.7元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com