练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】定义在上的函数，若满足:对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界

    （1）设，判断在上是否是有界函数，若是，说明理由，并写出所有上界的值的集合；若不是，也请说明理由.

    （2）若函数在上是以为上界的有界函数，求实数的取值范围.

    【答案】（1）是有界函数;（2）

    【解析】

    （1）分离常数后,可得函数的单调性,在区间内求得最大值与最小值,即可根据有界函数的定义求得的取值范围.

    （2）根据有界函数定义,可得的值域.代入解析式可分离得的不等式组.利用换元法转化为二次不等式形式,结合恒成立条件,即可求得的取值范围.

    （1）

    则在上单调递增

    所以对任意满足

    而

    所以

    若恒成立,则

    即所有上界的值的集合为

    （2）函数在上是以为上界的有界函数

    根据有界函数定义,可知在上恒成立

    所以

    即

    化简变形可得

    令

    则在上恒成立

    即满足

    由二次函数性质可知,,当时,

    ,所以当时,

    即,

    故的取值范围为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

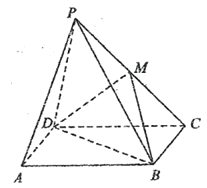
    【题目】如图，在四棱锥P—ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：

    （1）PA∥平面MDB；

    （2）PD⊥BC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆()的左右焦点分别为，为椭圆上位于轴同侧的两点，的周长为，的最大值为.

    (Ⅰ)求椭圆的方程；

    (Ⅱ)若，求四边形面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点是椭圆的右焦点，点，分别是轴，轴上的动点，且满足.若点满足（为坐标原点）．

    （Ⅰ）求点的轨迹的方程；

    （Ⅱ）设过点任作一直线与点的轨迹交于，两点，直线，与直线分别交于点，，试判断以线段为直径的圆是否经过点？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某镇有一块空地，其中，，.当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖，其中M，N都在边上，且，挖出的泥土堆放在地带上形成假山，剩下的地带开设儿童游乐场.为安全起见，需在的周围安装防护网.

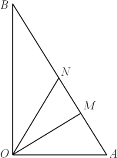
    （1）当时，求防护网的总长度；

    （2）为节省资金投入，人工湖的面积要尽可能小，设，问：当多大时的面积最小？最小面积是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l1：2x－y＋2＝0与l2：x＋2y－4＝0，点P(1, m)．

    （Ⅰ）若点P到直线l1, l2的距离相等，求实数m的值；

    （Ⅱ）当m＝1时，已知直线l经过点P且分别与l1, l2相交于A, B两点，若P恰好

    平分线段AB，求A, B两点的坐标及直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知实数x，y满足设，则z的取值范围是______.（表示a，b两数中的较大数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为常数.

    若曲线在处的切线斜率为-2，求该切线的方程；

    求函数在上的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若圆上至少有三个不同的点到直线的距离为，则直线l的倾斜角的取值范围是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    同步练习册答案