(本小题满分16分)已知常数
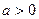
,函数
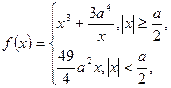
(1)求
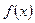
的单调递增区间;
(2)若
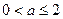
,求
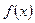
在区间
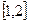
上的最小值
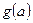
;
(3)是否存在常数
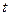
,使对于任意
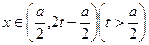
时,
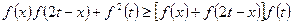
恒成立,若存在,求出
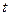
的值;若不存在,说明理由。
⑴当
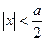
时,
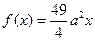
为增函数. …………………………………(1分)
当
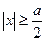
时,
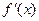
=
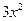
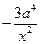
.令
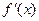
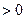
,得
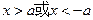
.…………(3分)
∴
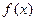
的增区间为

,
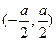
和
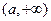
.……………………………(4分)
⑵由图可知,
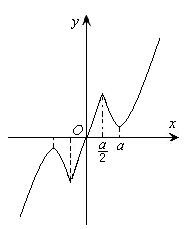
①当
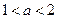
时,
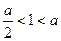
,
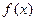
在区间
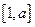
上递减,在
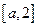
上递增,最小值为
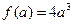
;………(6分)
②当
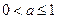
时,
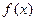
在区间
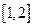
为增函数,最小值为
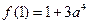
;……………………………(8分)
③当
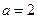
时,
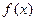
在区间
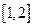
为增函数,最小值为
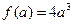
;……………………………(9分)
综上,
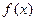
最小值
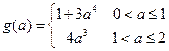
. ………………………………(10分)
⑶由
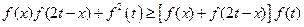
,
可得
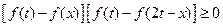
, ………………………………(12分)
即
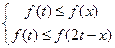
或
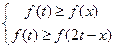
成立,所以
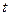
为极小值点,或
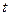
为极大值点.又
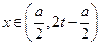
时
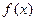
没有极大值,所以
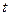
为极小值点,即
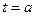
……………(16分)
(若只给出
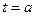
,不说明理由,得1分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
、已知定义域为
的函数
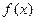
在
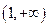
上为减函数,且函数
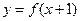
为偶函数,则( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(14分)
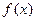
是定义在R上的函数,对
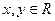
都有
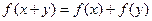
,且当
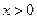
时,
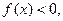
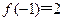
。
(1)求证:
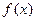
为奇函数;
(2)求证:
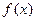
是R上的减函数;
(3)求
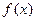
在
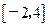
上的最值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
定义在
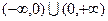
上的奇函数
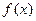
,在
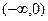
单调递增,且
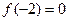
,则不等式
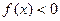
的解集是_________________
查看答案和解析>>

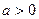 ,函数
,函数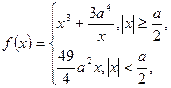
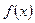 的单调递增区间;
的单调递增区间;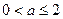 ,求
,求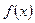 在区间
在区间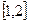 上的最小值
上的最小值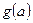 ;
;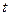 ,使对于任意
,使对于任意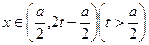 时,
时,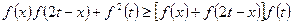 恒成立,若存在,求出
恒成立,若存在,求出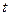 的值;若不存在,说明理由。
的值;若不存在,说明理由。 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案