
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
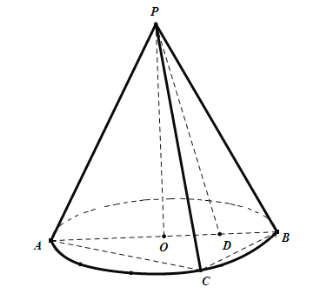
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A≠0,ω>0,![]() <φ<
<φ<![]() )的图象关于直线
)的图象关于直线![]() 对称,它的最小正周期为π,则( )
对称,它的最小正周期为π,则( )
A. f(x)的图象过点(0,![]() ) B. f(x)在
) B. f(x)在![]() 上是减函数
上是减函数
C. f(x)的一个对称中心是![]() D. f(x)的一个对称中心是
D. f(x)的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
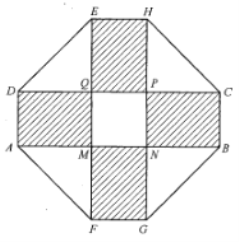
【题目】某小区要建一个八边形的休闲区,如图所示,它的主要造型平面图是由两个相同的矩形![]() 和
和![]() 构成的面积为
构成的面积为![]() 的十字形区域.计划在正方形
的十字形区域.计划在正方形![]() 上建一个花坛,造价为4200元/
上建一个花坛,造价为4200元/![]() ,在四个相同的矩形(图中阴影部分)上铺设花岗岩地面,造价为210元/
,在四个相同的矩形(图中阴影部分)上铺设花岗岩地面,造价为210元/![]() ,再在四个等腰直角三角形上铺设草坪,造价为80元/
,再在四个等腰直角三角形上铺设草坪,造价为80元/![]() .求当
.求当![]() 的长度为多少时,建设这个休闲区的总价最低.
的长度为多少时,建设这个休闲区的总价最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下的2×2列联表.已知在全部105人中抽到随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可能性要求,能否认为“成绩与班级有关系”?
P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式及数据:K2=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com