
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
(1)求cos(α﹣β)的值;
(2)若0<α< ![]() ,﹣
,﹣ ![]() <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
【答案】
(1)解:因为向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]() =
= ![]() =
= ![]() ,所以2﹣2cos(α﹣β)=
,所以2﹣2cos(α﹣β)= ![]() ,
,
所以cos(α﹣β)= ![]()
(2)解:若0<α< ![]() ,﹣
,﹣ ![]() <β<0,所以0<α﹣β<π,因为cos(α﹣β)=
<β<0,所以0<α﹣β<π,因为cos(α﹣β)= ![]() ,所以sin(α﹣β)=
,所以sin(α﹣β)= ![]()
且sinβ=﹣ ![]() ,cosβ=
,cosβ= ![]() ,
,
所以,sinα=sin(α﹣β+β)=sin(α﹣β)cosβ+cos(α﹣β)sinβ= ![]() =
= ![]()
【解析】(1)通过| ![]() ﹣
﹣ ![]() |=
|= ![]() .求出向量的模,化简即可求出cos(α﹣β)的值;(2)通过0<α<
.求出向量的模,化简即可求出cos(α﹣β)的值;(2)通过0<α< ![]() ,﹣
,﹣ ![]() <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ![]() ,求出cosβ的值,sin(α﹣β)的值,利用sinα=sin(α﹣β+β),然后求sinα的值.
,求出cosβ的值,sin(α﹣β)的值,利用sinα=sin(α﹣β+β),然后求sinα的值.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() 的半圆形铁皮上截取一块矩形材料ABCD(点A、B在直径上,点C、D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗),
的半圆形铁皮上截取一块矩形材料ABCD(点A、B在直径上,点C、D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗),
(1)若要求圆柱体罐子的侧面积最大,应如何截取?
(2)若要求圆柱体罐子的体积最大,应如何截取?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2﹣a=0(a∈R)
(1)若直线l在两坐标轴上的截距相等,则直线l的方程是;
(2)若直线l不经过第二象限,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
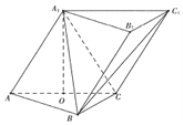
(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求三棱锥C1﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
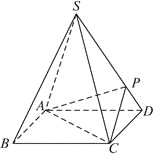
(1)求证:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若函数f(x)满足条件:存在[a,b]D,使f(x)在[a,b]上的值域是[2a,2b],则称f(x)为“倍扩函数”,若函数f(x)=log2(2x+t)为“倍扩函数”,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C:x2+y2=4和直线l:x=4,M为l上一动点,A1 , A2为圆C与x轴的两个交点,直线MA1 , MA2与圆C的另一个交点分别为P、Q.
(1)若M点的坐标为(4,2),求直线PQ方程;
(2)求证直线PQ过定点,并求出此定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com