
【题目】汽车尾气中含有一氧化碳![]() ,碳氢化合物
,碳氢化合物![]() 等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气之中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废,某环境组织为了解公众对机动车强制报废标准的了解情况,随机调查了
等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气之中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废,某环境组织为了解公众对机动车强制报废标准的了解情况,随机调查了![]() 人,所得数据制成如下列联表:
人,所得数据制成如下列联表:

(1)若从这![]() 人中任选
人中任选![]() 人,选到了解强制报废标准的人的概率为
人,选到了解强制报废标准的人的概率为![]() ,问是否在犯错的概率不超过5﹪的前提下认为“机动车强制报废标准是否了解与性别有关”?
,问是否在犯错的概率不超过5﹪的前提下认为“机动车强制报废标准是否了解与性别有关”?
(2)该环保组织从相关部门获得某型号汽车的使用年限与排放的尾气中![]() 浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过
浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过![]() 年,可近似认为排放的尾气中
年,可近似认为排放的尾气中![]() 浓度
浓度![]() ﹪与使用年限
﹪与使用年限![]() 线性相关,确定
线性相关,确定![]() 与
与![]() 的回归方程,并预测该型号的汽车使用
的回归方程,并预测该型号的汽车使用![]() 年排放尾气中的
年排放尾气中的![]() 浓度是使用
浓度是使用![]() 年的多少倍.
年的多少倍.

附:![]() ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)可以在犯错的概率不超过5﹪的前提下认为“机动车强制报废标准是否了解与性别有关”(2)![]() ;预测该型号的汽车使用12年排放尾气中的
;预测该型号的汽车使用12年排放尾气中的![]() 浓度是使用4年的4.2倍.
浓度是使用4年的4.2倍.
【解析】
(1)根据题意计算![]() ,再利用
,再利用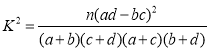 ,计算出
,计算出![]() ,对照临界值得出结论;(2)由公式计算出
,对照临界值得出结论;(2)由公式计算出![]() ,可得y关于t的回归方程,把t=12代入回归方程中,可预测该型号的汽车使用12年排放尾气中的
,可得y关于t的回归方程,把t=12代入回归方程中,可预测该型号的汽车使用12年排放尾气中的![]() 浓度,即得。
浓度,即得。
(1)设“从100人中任选1人,选到了解机动车强制报废标准的人”为事件![]() ,
,
由已知得![]() ,解得
,解得![]() ,所以
,所以![]() ,
,![]() ,
,![]() .
.
假设![]() :机动车强制报废标准是否了解与性别无关.
:机动车强制报废标准是否了解与性别无关.
由2×2列联表可知,![]() 的观测值
的观测值![]() ,
,
∴可以在犯错的概率不超过5﹪的前提下认为“机动车强制报废标准是否了解与性别有关”
(2)由折线图中所给数据计算,得![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,
所以所求回归方程为![]() .
.
故预测该型号的汽车使用12年排放尾气中的![]() 浓度为
浓度为![]() ,
,
因为使用4年排放尾气中的![]() 浓度为
浓度为![]() ,
,
所以预测该型号的汽车使用12年排放尾气中的![]() 浓度是使用4年的4.2倍.
浓度是使用4年的4.2倍.


科目:高中数学 来源: 题型:
【题目】二次函数![]() 图像与
图像与![]() 轴交于
轴交于![]() ,
,![]() 两点,交直线
两点,交直线![]() 于
于![]() ,
,![]() 两点,经过三点
两点,经过三点![]() ,
,![]() ,
,![]() 作圆
作圆![]() .
.
(1)求证:当![]() 变化时,圆
变化时,圆![]() 的圆心在一条定直线上;
的圆心在一条定直线上;
(2)求证:圆![]() 经过除原点外的一个定点.
经过除原点外的一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学届的震动。在1859年的时候,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想。在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,
的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市委积极响应十九大报告提出的“到2020年全面建成小康社会”的目标,鼓励各县积极脱贫,计划表彰在农村脱贫攻坚战中的杰出村代表,已知A,B两个贫困县各有15名村代表,最终A县有5人表现突出,B县有3人表现突出,现分别从A,B两个县的15人中各选1人,已知有人表现突出,则B县选取的人表现不突出的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元;
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、l个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(1)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(2)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a-![]() )x2-2ax+lnx,a∈R
)x2-2ax+lnx,a∈R
(1)当a=1时,求f(x)在区间[1,e]上的最大值和最小值;
(2)求g(x)=f(x)+ax在x=1处的切线方程;
(3)若在区间(1,+∞)上,f(x)<0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为
的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com