
【题目】已知椭圆![]() 的两焦点为
的两焦点为![]() ,
,![]() ,且过点
,且过点![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 不过点
不过点![]() 且不平行于坐标轴,记线段
且不平行于坐标轴,记线段![]() 的中点为
的中点为![]() ,求证:直线
,求证:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)若直线![]() 过点
过点![]() ,求
,求![]() 面积的最大值,以及取最大值时直线
面积的最大值,以及取最大值时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)见解析 (3)最大值
(2)见解析 (3)最大值![]() .
.![]()
【解析】
(1)根据焦点求得![]() ,结合
,结合![]() 点坐标列方程组,解方程组求得
点坐标列方程组,解方程组求得![]() ,进而求得椭圆的标准方程.
,进而求得椭圆的标准方程.
(2)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,写出韦达定理,由此计算出
的方程和椭圆方程,写出韦达定理,由此计算出![]() 为定值.
为定值.
(3)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,写出韦达定理,根据弦长公式和点到直线的距离公式,求得
的方程和椭圆方程,写出韦达定理,根据弦长公式和点到直线的距离公式,求得![]() 面积的表达式,利用换元法,结合基本不等式求得面积的最大值,以及此时直线
面积的表达式,利用换元法,结合基本不等式求得面积的最大值,以及此时直线![]() 的方程.
的方程.
(1)由题意知有![]() ,且
,且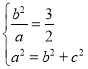 ,解得
,解得![]() ,∴
,∴![]() .
.
(2)证明:设直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
则由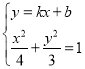 可得
可得![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
![]() ,
,
![]() ,
,
∴直线![]() 的斜率与
的斜率与![]() 的斜率的乘积
的斜率的乘积![]() 为定值.
为定值.
(3)点![]() ,
,![]() ,
,
由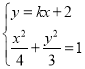 可得
可得![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,
∴![]()
 .
.
设![]() ,
,![]() ,
,
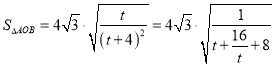 ,
,
![]() ,
,
当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
此时![]() ,即
,即![]() ,
,
所以直线方程是![]() .
.


科目:高中数学 来源: 题型:
【题目】某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.

(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF 面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF
连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
表![]()
图![]()
(I)根据表![]() ,是否有
,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
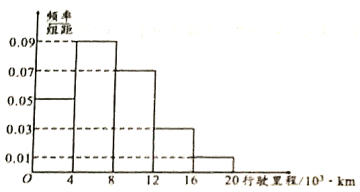
(II)图![]() 给出的是
给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(III)用表![]() 中的频率估计概率,随机调查
中的频率估计概率,随机调查![]() 名
名![]() 岁以下车主,设其中购买了轿车的人数为
岁以下车主,设其中购买了轿车的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个不同的红球和
个不同的红球和![]() 个不同的白球,放入同一个袋中,现从中取出
个不同的白球,放入同一个袋中,现从中取出![]() 个球.
个球.
(1)若取出的红球的个数不少于白球的个数,则有多少种不同的取法;
(2)取出一个红球记![]() 分,取出一个白球记
分,取出一个白球记![]() 分,若取出
分,若取出![]() 个球的总分不少于
个球的总分不少于![]() 分,则有多少种不同的取法;
分,则有多少种不同的取法;
(3)若将取出的![]() 个球放入一箱子中,记“从箱子中任意取出
个球放入一箱子中,记“从箱子中任意取出![]() 个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到
个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到![]() 个红球并且恰有一次取到
个红球并且恰有一次取到![]() 个白球的概率.
个白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,中国某省的一个地区社会民间组织为年龄在30岁-60岁的围棋爱好者举行了一次晋级赛,参赛者每人和一位种子选手进行一场比赛,赢了就可以晋级,否则,就不能晋级,结果将晋级的200人按年龄(单位:岁)分成六组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,第六组
,第六组![]() ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.
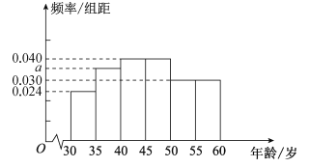
(1)求实数![]() 的值;
的值;
(2)若先在第四组、第五组、第六组中按组分层抽样共抽取10人,然后从被抽取的这10人中随机抽取3人参加优胜比赛.
①求这三组各有一人参加优胜比赛的概率;
②设![]() 为参加优胜比赛的3人中第四组的人数,求
为参加优胜比赛的3人中第四组的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,A(0,1),AB边上的高CD所在直线的方程为x+2y-4=0,AC边上的中线BE所在直线的方程为2x+y-3=0.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() .
.
(Ⅰ)![]() 、
、![]() 是抛物线
是抛物线![]() 上不同于顶点
上不同于顶点![]() 的两点,若以
的两点,若以![]() 为直径的圆经过抛物线的顶点,试证明直线
为直径的圆经过抛物线的顶点,试证明直线![]() 必过定点,并求出该定点的坐标;
必过定点,并求出该定点的坐标;
(Ⅱ)在(Ⅰ)的条件下,抛物线在![]() 、
、![]() 处的切线相交于点
处的切线相交于点![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com