
【题目】以直角坐标系xOy的坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是![]() ,曲线C2的参数方程是
,曲线C2的参数方程是![]() (θ为参数).
(θ为参数).
(1)写出曲线C1,C2的普通方程;
(2)设曲线C1与y轴相交于A,B两点,点P为曲线C2上任一点,求|PA|2+|PB|2的取值范围.
【答案】(1) 曲线C1的普通方程为![]() .曲线C2的普通方程为(x-2)2+(y-2)2=4.(2) [32-16
.曲线C2的普通方程为(x-2)2+(y-2)2=4.(2) [32-16![]() ,32+16
,32+16![]() ].
].
【解析】
(1)由题得![]() ,再把极坐标化成直角坐标,得到C1的普通方程;消参得到C2的普通方程;(2)设P(2+2cosθ,2+2sinθ),求出|PA|2+|PB|2=
,再把极坐标化成直角坐标,得到C1的普通方程;消参得到C2的普通方程;(2)设P(2+2cosθ,2+2sinθ),求出|PA|2+|PB|2=![]()
![]() ,再求其取值范围.
,再求其取值范围.
(1)由![]() ,得
,得![]() .
.
∴![]() ,4ρ2cos2θ+9ρ2sin2θ=36.∴4x2+9y2=36,
,4ρ2cos2θ+9ρ2sin2θ=36.∴4x2+9y2=36,
即曲线C1的普通方程为![]() .
.
曲线C2的普通方程为(x-2)2+(y-2)2=4.
(2)由(1)知,点A,B的坐标分别为(0,2),(0,-2),设P(2+2cosθ,2+2sinθ),
则|PA|2+|PB|2=(2+2cosθ)2+(2sinθ)2+(2+2cosθ)2+(4+2sinθ)2=32+16sinθ+16cosθ![]() .
.
∴|PA|2+|PB|2∈[32-16![]() ,32+16
,32+16![]() ],
],
即|PA|2+|PB|2的取值范围是[32-16![]() ,32+16
,32+16![]() ].
].


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex![]() (x﹣a)2+4.
(x﹣a)2+4.
(1)若f(x)在(﹣∞,+∞)上单调递增,求a的取值范围;
(2)若x≥0,不等式f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.

(1)求证:PA//平面MBD.
(2)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,P是椭圆上位于第一象限内的点,
,P是椭圆上位于第一象限内的点,![]() 轴,垂足为Q,
轴,垂足为Q,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
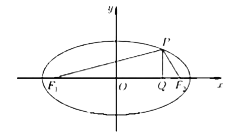
(1)求椭圆F的方程:
(2)若M是椭圆上的动点,求![]() 的最大值,并求出
的最大值,并求出![]() 取得最大值时M的坐标.
取得最大值时M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“紧密”数列.
为“紧密”数列.
(1)设某个数列为“紧密”数列,其前![]() 项依次为
项依次为![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若数列![]() 的前项和
的前项和![]() ,判断
,判断![]() 是否为“紧密”数列,并说明理由;
是否为“紧密”数列,并说明理由;
(3)设![]() 是公比为
是公比为![]() 的等比数列,前
的等比数列,前![]() 项和为
项和为![]() ,且
,且![]() 与
与![]() 均为“紧密”数列,求实数
均为“紧密”数列,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com