
【题目】如图,在三棱锥S﹣ABC中,∠ABC=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为E、D. 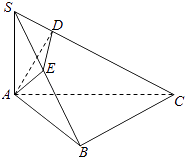
(1)求证:DE⊥SC;
(2)若SA=AB=BC=1,求直线AD与平面ABC所成角的余弦值. 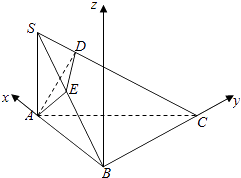
【答案】
(1)证明:∵SA⊥平面ABC,BC平面ABC,
∴SA⊥BC,
∵∠ABC=90°,即AB⊥BC,AB∩SA=A,
∴BC⊥平面SAB.
∵AE平面SAB,∴BC⊥AE.
∵AE⊥SB,SB∩BC=B,∴AE⊥平面SBC,
∵SC平面SBC,∴AE⊥SC,
又∵AD⊥SC,AD∩AE=A,
∴SC⊥平面ADE,DE平面SBC,
∴DE⊥SC.
(2)解:以B为原点,BA为x轴,BC为y轴,过B作AS的平行线为z轴,建立空间直角坐标系,
A(1,0,0),S(1,0,1),C(0,1,0),
设D(a,b,c), ![]() ,则(a﹣1,b,c﹣1)=(﹣λ,λ,﹣λ),∴D(1﹣λ,λ,1﹣λ),
,则(a﹣1,b,c﹣1)=(﹣λ,λ,﹣λ),∴D(1﹣λ,λ,1﹣λ),
∴ ![]() =(﹣1,1,﹣1),
=(﹣1,1,﹣1), ![]() =(﹣λ,λ,1﹣λ),
=(﹣λ,λ,1﹣λ),
∵点A在SC上的射影D,∴ ![]() =λ+λ﹣1+λ=0,解得
=λ+λ﹣1+λ=0,解得 ![]() ,
,
∴D( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ),
),
设直线AD与平面ABC所成角为θ,平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
则sinθ= 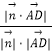 =
= 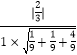 =
= ![]() ,
,
∴cosθ= ![]() =
= ![]() .
.
∴直线AD与平面ABC所成角的余弦值为 ![]()
【解析】(1)推导出SA⊥BC,AB⊥BC,从而BC⊥AE,再由AE⊥SC,能证明DE⊥SC.(2)以B为原点,BA为x轴,BC为y轴,过B作AS的平行线为z轴,建立空间直角坐标系,利用向量法能求出直线AD与平面ABC所成角的余弦值.
【考点精析】本题主要考查了直线与平面垂直的性质和空间角的异面直线所成的角的相关知识点,需要掌握垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则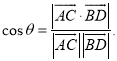 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点. 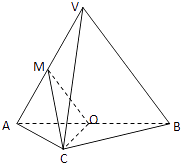
(1)求证:VB∥平面MOC.
(2)求证:平面MOC⊥平面VAB.
(3)求二面角C﹣VB﹣A的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x+1) ![]() ﹣
﹣ ![]() cos(x+1)
cos(x+1) ![]() ,则f(1)+f(2)+f(3)+…+f(2011)=( )
,则f(1)+f(2)+f(3)+…+f(2011)=( )
A.2 ![]()
B.![]()
C.﹣ ![]()
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y=0垂直.
(1)求实数a,b的值;
(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布图如图所示,下表是年龄的频率分布表.
,得到的频率分布图如图所示,下表是年龄的频率分布表.
![]()

(1)现要从年龄较小的第![]() 组中用分层抽样的方法抽取6人,则年龄第
组中用分层抽样的方法抽取6人,则年龄第![]() 组人数分别是多少?
组人数分别是多少?
(2)在(1)的条件下,从这6中随机抽取2参加社区宣传交流活动,求恰有2人在第3组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4名男生,3名女生排成一排:
(1)从中选出3人排成一排,有多少种排法?
(2)若男生甲不站排头,女生乙不站在排尾,则有多少种不同的排法?
(3)要求女生必须站在一起,则有多少种不同的排法?
(4)若3名女生互不相邻,则有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自然数按如图的规律排列:则上起第2007行左起2008列的数为( ) 
A.20072
B.20082
C.2006×2007
D.2007×2008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com