Question

15．设复数z=（x-1）+yi（x∈R，y≥0），若|z|≤1，则y≥x的概率为（　　）

• A． $\frac{3}{4}+\frac{1}{2π}$
• B． $\frac{1}{4}-\frac{1}{2π}$
• C． $\frac{1}{2}-\frac{1}{π}$
• D． $\frac{1}{2}+\frac{1}{π}$

Answer 1

分析 由题意易得所求概率为弓形的面积与圆的面积之比，分别求面积可得．

解答 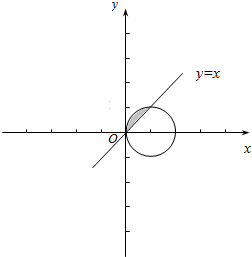解：∵复数z=（x-1）+yi（x，y∈R）且|z|≤1，
∴|z|=$\sqrt{（x-1）^{2}+{y}^{2}}$≤1，即（x-1）²+y²≤1，
∴点（x，y）在（1，0）为圆心1为半径的圆及其内部，
而y≥x表示直线y=x左上方的部分，（图中阴影弓形）
∴所求概率为弓形的面积与圆的面积一半的之比，
∴所求概率P=$\frac{\frac{1}{4}•π•{1}^{2}-\frac{1}{2}×1×1}{\frac{1}{2}•π•{1}^{2}}$=$\frac{1}{2}$-$\frac{1}{π}$
故选：C．

点评 本题考查几何概型，涉及复数以及圆的知识，属基础题．