
【题目】设![]() 、
、![]() 为两个不重合的平面,则
为两个不重合的平面,则![]() 的充要条件是( )
的充要条件是( )
A.![]() 内有无数条直线与
内有无数条直线与![]() 平行B.
平行B.![]() 、
、![]() 垂直于同一平面
垂直于同一平面
C.![]() 、
、![]() 平行于同一条直线D.
平行于同一条直线D.![]() 内有两条相交直线与
内有两条相交直线与![]() 平行
平行
科目:高中数学 来源: 题型:
【题目】用n种不同的颜色为下列两块广告牌着色,(如图甲、乙),要求在A,B,C,D四个区域中相邻(有公共边界)的区域不用同一颜色.
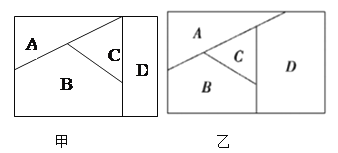
(1)若n=6,则为甲图着色时共有多少种不同的方法;
(2)若为乙图着色时共有120种不同方法,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在2018年社保又出新的好消息,之前流动就业人员跨地区就业后,社保转移接续的手续往往比较繁琐,费时费力.社保改革后将简化手续,深得流动就业人员的赞誉.某市社保局从2018年办理社保的人员中抽取300人,得到其办理手续所需时间(天)与人数的频数分布表:
时间 |
|
|
|
|
|
|
人数 | 15 | 60 | 90 | 75 | 45 | 15 |
(1)若300名办理社保的人员中流动人员210人,非流动人员90人,若办理时间超过4天的人员里非流动人员有60人,请完成办理社保手续所需时间与是否流动人员的列联表,并判断是否有95%的把握认为“办理社保手续所需时间与是否流动人员”有关.
列联表如下
流动人员 | 非流动人员 | 总计 | |
办理社保手续所需 时间不超过4天 | |||
办理社保手续所需 时间超过4天 | 60 | ||
总计 | 210 | 90 | 300 |
(2)为了改进工作作风,提高效率,从抽取的300人中办理时间为![]() 流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为
流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为![]() 的人数为
的人数为![]() ,求出
,求出![]() 分布列及期望值.
分布列及期望值.
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为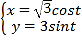 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间某商店出售某种海鲜礼盒,假设每天该礼盒的需求量在![]() 范围内等可能取值,该礼盒的进货量也在
范围内等可能取值,该礼盒的进货量也在![]() 范围内取值(每天进1次货).商店每销售1盒礼盒可获利50元;若供大于求,剩余的削价处理,每处理1盒礼盒亏损10元;若供不应求,可从其它商店调拨,销售1盒礼盒可获利30元.设该礼盒每天的需求量为
范围内取值(每天进1次货).商店每销售1盒礼盒可获利50元;若供大于求,剩余的削价处理,每处理1盒礼盒亏损10元;若供不应求,可从其它商店调拨,销售1盒礼盒可获利30元.设该礼盒每天的需求量为![]() 盒,进货量为
盒,进货量为![]() 盒,商店的日利润为
盒,商店的日利润为![]() 元.
元.
(1)求商店的日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)试计算进货量![]() 为多少时,商店日利润的期望值最大?并求出日利润期望值的最大值.
为多少时,商店日利润的期望值最大?并求出日利润期望值的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com