设函数f(x)的定义域为R,对于任意实数m、n,总有f(m+n)=f(m)•f(n),且x>0时0<f(x)<1.
(1)证明:f(0)=1,且x<0时f(x)>1;
(2)证明:f(x)在R 上单调递减;
(3)设A={(x,y)|f(x2)•f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=∅,确定a 的范围.
解:(1)证明:f(m+n)=f(m)•f(n),
令m>0,n=0,?f(m)=f(m)f(0)
已知x>0时0<f(x)<1.
?f(0)=1
设m=x<0,n=-x>0,f(-x)∈(0,1)
?f(0)=f(m+n)=f(m)f(n)=1?f(m)>1,即当x<0时f(x)>1 …(4分)
(2)?x
1<x
2∈R,则x
2-x
1>0,0<f(x
2-x
1)<1,f(x
1)>0?f(x
2)-f(x
1)
=f(x
2-x
1+x
1)-f(x
1)=f(x
2-x
1)f(x
1)-f(x
1)=f(x
1)[f(x
2-x
1)-1]<0
∴f(x)在R 上单调递减. …(10分)
(3)f(x
2)f(y
2)>f(1)?f(x
2+y
2)>f(1)
f(x)在R上单调递减
?x
2+y
2<1(单位圆内部分)
f(ax-y+2)=1=f(0)?ax-y+2=0(一条直线)
A∩B=φ?
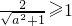
?a2≤3?a∈[

,

]…(16分)
分析:对于抽象函数的求解策略和方法为赋值法,
(1)令m>0,n=0,代入已知条件,即可求得结果;
(2))?x
1<x
2∈R,则x
2-x
1>0,0<f(x
2-x
1)<1,f(x
1)>0?f(x
2)-f(x
1)=f(x
2-x
1+x
1)-f(x
1)=f(x
2-x
1)f(x
1)-f(x
1)=f(x
1)[f(x
2-x
1)-1]<0代入已知条件即可判定函数的单调性.
(3)f(x
2)f(y
2)>f(1)?f(x
2+y
2)>f(1)结合函数f(x)在R上单调递减得到x
2+y
2<1;f(ax-y+2)=1=f(0)?ax-y+2=0(一条直线)结合直线与圆的位置关系即可确定a 的范围.
点评:本题考查抽象函数的有关问题,其中赋值法是常用的方法,考查函数单调性的判断与证明、函数的奇偶性的定义,属基础题.

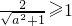 ?a2≤3?a∈[
?a2≤3?a∈[ ,
, ]…(16分)
]…(16分)

 )与b=f(
)与b=f( )的大小关系为________.
)的大小关系为________. )与b=f(
)与b=f( )的大小关系为 .
)的大小关系为 . )与b=f(
)与b=f( )的大小关系为( ).
)的大小关系为( ).