
分析 由题意化简可得圆的标准方程,从而作图象,而(x-m)2+(y-n)2的几何意义是两圆上的点的距离的平方,从而利用图象求解.
解答 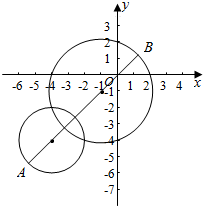 解:∵x2+y2+2x+2y-8=0,
解:∵x2+y2+2x+2y-8=0,
∴(x+1)2+(y+1)2=10,
∵m2+n2+8m+8n+28=0,
∴(m+4)2+(n+4)2=4;
作其图象如右图,
(x-m)2+(y-n)2的几何意义是两圆上的点的距离的平方,
|AB|=2+$\sqrt{10}$+3$\sqrt{2}$,
故(x-m)2+(y-n)2的最大值为(2+$\sqrt{10}$+3$\sqrt{2}$)2,
最小值为0.
故答案为:(2+$\sqrt{10}$+3$\sqrt{2}$)2,0.
点评 本题考查了数形结合的思想应用及学生的化简运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
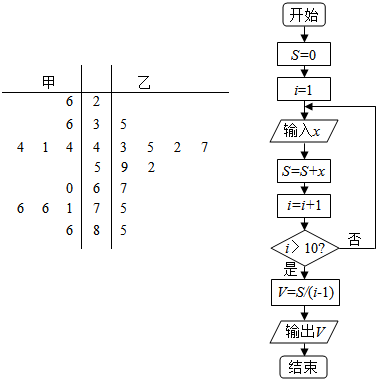 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com