


科目:高中数学 来源: 题型:
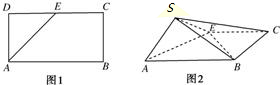
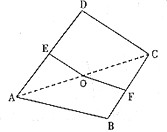 如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )
如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )| A、30° | B、60° | C、120° | D、150° |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
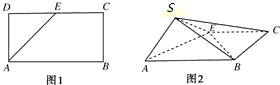
查看答案和解析>>
科目:高中数学 来源:2008-2009学年福建省泉州市惠安县惠南中学高二(上)期末数学试卷(选修2-1)(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2011年山西省高三考前适应性训练数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com