
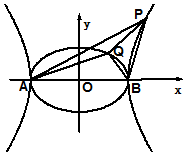
 已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )
已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )| A. | 大于0 | B. | 等于0 | ||
| C. | 小于0 | D. | 大于0,等于0,小于0都有可能 |
分析 设P(x1,y1)、Q(x2,y2),利用斜率公式得到k1+k2=$\frac{{y}_{1}}{{x}_{1}+2}$+$\frac{{y}_{1}}{{x}_{1}-2}$=$\frac{{x}_{1}}{2{y}_{1}}$;同理可得k3+k4=-$\frac{{x}_{2}}{2{y}_{2}}$,结合O、P、Q三点共线即可得出k1+k2+k3+k4的值.
解答 解:由题意,O、P、Q三点共线.
设P(x1,y1)、Q(x2,y2),
点P在双曲线$\frac{x^2}{4}-{y^2}$=1上,有x12-4=4y12.
所以k1+k2=$\frac{{y}_{1}}{{x}_{1}+2}$+$\frac{{y}_{1}}{{x}_{1}-2}$=$\frac{{x}_{1}}{2{y}_{1}}$. ①
又由点Q在椭圆$\frac{x^2}{4}+{y^2}$=1上,有x22-4=-2y22.
同理可得k3+k4=-$\frac{{x}_{2}}{2{y}_{2}}$②
∵O、P、Q三点共线.
∴$\frac{{x}_{1}}{{y}_{1}}$=$\frac{{x}_{2}}{{y}_{2}}$.
由①、②得k1+k2+k3+k4=0.
故选B.
点评 本小题主要考查椭圆的几何性质、双曲线的几何性质、圆锥曲线的综合等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{1}{8}$ | C. | 3 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com