
【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
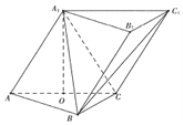
(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求三棱锥C1﹣ABC的体积.
【答案】(Ⅰ)见解析; (Ⅱ)1.
【解析】试题分析:(Ⅰ)由面面垂直的判定定理证明;(Ⅱ)因为![]() 平面
平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,而由(Ⅰ)有:A1O⊥平面ABC,所以
的距离,而由(Ⅰ)有:A1O⊥平面ABC,所以![]() 为点
为点![]() 到平面
到平面![]() 的距离,再用椎体体积公式求出体积.
的距离,再用椎体体积公式求出体积.
试题解析:证明:(Ⅰ)∵AA1=A1C,且O为AC的中点,
∴A1O⊥AC,
又∵平面AA1C1C⊥平面ABC,
平面AA1C1C∩平面ABC=AC
且A1O平面AA1C1C,
∴A1O⊥平面ABC
(Ⅱ)∵A1C1∥AC,A1C1平面ABC,AC平面ABC,
∴A1C1∥平面ABC,
即C1到平面ABC的距离等于A1到平面ABC的距离
由(Ⅰ)知A1O⊥平面ABC且![]() ,
,
∴三棱锥C1﹣ABC的体积:
![]()


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
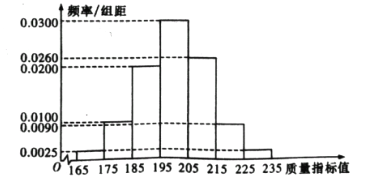
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在坐标原点,且与直线l1:x﹣y﹣2 ![]() =0相切 (Ⅰ)求直线l2:4x﹣3y+5=0被圆C所截得的弦AB的长.
=0相切 (Ⅰ)求直线l2:4x﹣3y+5=0被圆C所截得的弦AB的长.
(Ⅱ)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N,求直线MN的方程
(Ⅲ) 若与直线l1垂直的直线l与圆C交于不同的两点P,Q,若∠POQ为钝角,求直线l纵截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
(1)求cos(α﹣β)的值;
(2)若0<α< ![]() ,﹣
,﹣ ![]() <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①若f(x)=ax2+(2a+b)x+2(其中x∈[﹣1,a])是偶函数,则实数b=﹣2;
②f(x)= ![]() +
+ ![]() 既是奇函数又是偶函数;
既是奇函数又是偶函数;
③若f(x+2)= ![]() ,当x∈(0,2)时,f(x)=2x , 则f(2015)=2;
,当x∈(0,2)时,f(x)=2x , 则f(2015)=2;
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),则f(x)是奇函数.其中所有正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com