
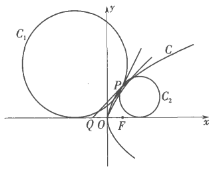
【题目】如图,在平面直角坐标系xOy中,F为x轴正半轴上的一个动点.以F为焦点、O为顶点作抛物线C.设P为第一象限内抛物线C上的一点,Q为x轴负半轴上一点,使得PQ为抛物线C的切线,且![]() .圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
.圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
科目:高中数学 来源: 题型:
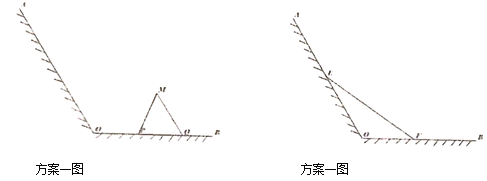
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,离心率
的左、右焦点分别为F1,F2,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)求椭圆的标准方程;
(2)已知直线l1,l2过右焦点F2,且它们的斜率乘积为﹣1,设l1,l2分别与椭圆交于点A,B和C,D.①求AB+CD的值;②设AB的中点M,CD的中点为N,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试中500名学生的物理(满分为150分)成绩服从正态分布![]() ,数学成绩的频率分布直方图如图所示.
,数学成绩的频率分布直方图如图所示.

(Ⅰ)如果成绩大于135分为特别优秀,那么本次考试中的物理、数学特别优秀的大约各有多少人?
(Ⅱ)如果物理和数学两科都特别优秀的共有4人,是否有99.9%的把握认为物理特别优秀的学生,数学也特别优秀?
附:①若![]() ,则
,则![]()
②表及公式:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.

(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推进“千村百镇计划”,2019年4月某新能源公司开展“电动绿色出行”活动,首批投放200台![]() 型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
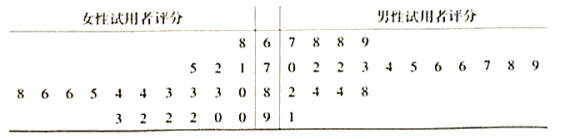
(1)求40个样本数据的中位数![]() ;
;
(2)已知40个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中,评分小于![]() 的份数;
的份数;
②请根据40个样本数据,完成下面2×2列联表:
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关?
附: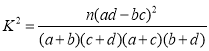 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com