
已知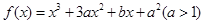 在
在 时有极值0。
时有极值0。
(1)求常数
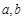 的值;
的值;
(2)求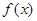 的单调区间。
的单调区间。
(3)方程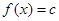 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数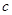 的范围。
的范围。
(1)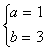 (舍去)或
(舍去)或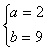 ;
;
(2)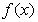 的减函数区间为
的减函数区间为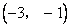 ,
, 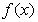 的增函数区间为
的增函数区间为 或
或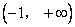 ;
;
(3) 。
。
【解析】
试题分析:(1)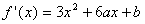 ,由题知:
,由题知:
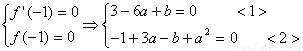 2分
2分
联立<1>、<2>有: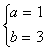 (舍去)或
(舍去)或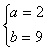 4分
4分
(2)当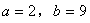 时,
时,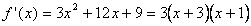
故方程 有根
有根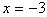 或
或 6分
6分
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↑ |
极大值 |
↓ |
极小值 |
↑ |
由表可见,当 时,
时,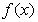 有极小值0,故
有极小值0,故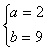 符合题意
8分
符合题意
8分
由上表可知: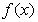 的减函数区间为
的减函数区间为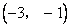
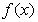 的增函数区间为
的增函数区间为 或
或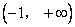 10分
10分
(3)因为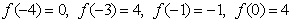 ,
,
由数形结合可得 。
。
考点:本题主要考查应用导数研究函数的单调性及极(最)值,研究函数的图象和性质,方程的根。
点评:中档题,属于导数应用的基本问题。(II)(III)两小题,通过研究函数的单调性、极值(最值),认识函数图象的变化形态等,寻求得到解题途径。有一定技巧性,对学生要求较高。


科目:高中数学 来源:2013届安徽省高二3月月考理科数学试卷 题型:解答题
.已知 在
在 时有极值0.
时有极值0.
①求常数  的值;
的值;
②求 的单调区间;
的单调区间;
③方程 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数 的范围.
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com