练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．若无穷等差数列{an}的首项a1＞0，公差d＜0，{an}的前n项和为Sn，则（　　）
    A．Sn单调递减B．Sn单调递增C．Sn有最大值D．Sn有最小值

    分析 化简可得{an}是递减数列，且先正值，后负值；从而判断出Sn有最大值．

    解答 解：∵无穷等差数列{an}的首项a1＞0，公差d＜0，
    ∴{an}是递减数列，且先正值，后负值；
    ∴{an}的前n项和为Sn先增加，后减小；
    ∴Sn有最大值；
    故选C．

    点评 本题考查了单调性数列的应用及前n项和的最值的判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．若loga（3a-2）是正数，则实数a的取值范围是$（{\frac{2}{3}，1}）∪（{1，+∞}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．含有甲、乙、丙的六位同学站成一排，则甲、乙相邻且甲、丙两人中间恰有两人的站法的种数为（　　）
    A．72B．60C．32D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知椭圆$\frac{{x}^{2}}{10-m}$+$\frac{{y}^{2}}{m-2}$=1的长轴在y轴上，若焦距为4，则m=8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某企业为打入国际市场，决定从A、B两种产品中只选择一种进行投资生产．已知投资生产这两种产品的有关数据如下表：（单位：万美元）

    项目
    类别    		年固定
    成本    		每件产品
    成本    		每件产品
    销售价    		每年最多可
    生产的件数
    A产品20m10200
    B产品40818120
    其中年固定成本与年生产的件数无关，c为待定常数，其值由生产A产品的原材料价格决定，预计c∈[6，9]另外，年销售x件B产品时需上交0.05x2万美元的特别关税．假设生产出来的产品都能在当年销售出去．
    （1）写出该厂分别投资生产A、B两种产品的年利润y1，y2与生产相应产品的件数x之间的函数关系并指明其定义域；
    （2）如何投资最合理（可获得最大年利润）？请你做出规划．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．函数f（x）与g（x）的图象拼成如图所示的“Z”字形折线段ABOCD，不含A（0，1），B（1，1），O（0，0），C（-1，-1），D（0，-1）五个点，若f（x）的图象关于原点对称的图形即为g（x）的图象，则其中一个函数的解析式可以为f（x）=$\left\{\begin{array}{l}{x，-1＜x＜0}\\{1，0＜x＜1}\end{array}\right.$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知钝角△ABC的面积为2$\sqrt{3}$，AB=2，BC=4，则该三角形的外接圆半径为$\frac{2\sqrt{21}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．函数$y={3^{{x^2}-1}}（-1≤x＜0）$的反函数是（　　）
    A．$y=-\sqrt{1+{{log}_3}x}（x≥\frac{1}{3}）$B．$y=-\sqrt{1+{{log}_3}x}（\frac{1}{3}＜x≤1）$
    C．$y=\sqrt{1+{{log}_3}x}（\frac{1}{3}＜x≤1）$D．$y=\sqrt{1+{{log}_3}x}（x≥\frac{1}{3}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

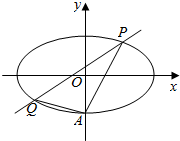    14．如图，椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点A（0，-1），且离心率为$\frac{\sqrt{2}}{2}$．
    （I）求椭圆E的方程；
    （II）经过点（1，1），且斜率为k的直线与椭圆E交于不同两点P，Q（均异于点A），问直线AP与AQ的斜率之和是否为定值，若是，求出这个定值；若不是，请说明理由．

    查看答案和解析>>

    同步练习册答案