
【题目】在平面直角坐标系xOy中,椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且与直线
,1),且与直线 ![]() x+2y﹣4=0相切.
x+2y﹣4=0相切.
(1)求椭圆E的方程;
(2)若椭圆E与x轴交于M、N两点,椭圆E内部的动点P使|PM|、|PO|、|PN|成等比数列,求 ![]()
![]() 的取值范围.
的取值范围.
【答案】
(1)解:∵椭圆E: ![]() (a>b>0)与直线
(a>b>0)与直线 ![]() x+2y﹣4=0相切,联立
x+2y﹣4=0相切,联立 ![]() ,
,
整理得( ![]() )x2﹣2
)x2﹣2 ![]() a2x+4a2﹣a2b2=0,
a2x+4a2﹣a2b2=0,
由△=0,可得 ![]() …①
…①
∵椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),∴
,1),∴ ![]() …②
…②
由①②得a2=4,b2=2.∴椭圆E的方程: ![]()
(2)解:由(1)得M(﹣2,0))、PN(2,0),设P(m,n)
∵|PM|、|PO|、|PN|成等比数列,
∴|PO|2=|PN||PM|(m2+n2)2= ![]()
m2=n2+2,…③
∵ ![]() ,∴
,∴ ![]() =2n2﹣2
=2n2﹣2
∵P在椭圆E内部,∴0≤n2<1,
∴ ![]() .即
.即 ![]()
![]() 的取值范围为[﹣2,0)
的取值范围为[﹣2,0)
【解析】(1)由椭圆E: ![]() (a>b>0)与直线
(a>b>0)与直线 ![]() x+2y﹣4=0相切,联立
x+2y﹣4=0相切,联立 ![]() ,由△=0,可得
,由△=0,可得 ![]() …①,由椭圆E:
…①,由椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),∴
,1),∴ ![]() …②,由①②得a2 , b2(2)设P(m,n),由|PO|2=|PN||PM|(m2+n2)2=
…②,由①②得a2 , b2(2)设P(m,n),由|PO|2=|PN||PM|(m2+n2)2= ![]() m2=n2+2, ∴
m2=n2+2, ∴ ![]() =2n2﹣2,由n的范围求得其范围,
=2n2﹣2,由n的范围求得其范围,
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知菱形 ABCD 中,对角线 AC 与 BD 相交于一点 O,∠A=60°,将△BDC 沿着 BD 折起得△BDC',连结 AC'.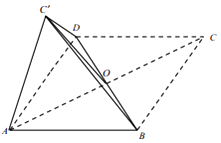
(Ⅰ)求证:平面 AOC'⊥平面 ABD;
(Ⅱ)若点 C'在平面 ABD 上的投影恰好是△ABD 的重心,求直线 CD 与底面 ADC'所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC=a,AC=b,且a,b是方程![]() 的两根,2cos(A+B)=1.
的两根,2cos(A+B)=1.
(1)求∠C的度数;
(2)求AB的长;
(3)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体ABCD的顶点都在球O表面上,且AB=BC=AC=2 ![]() ,DA=DB=DC=2,过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则( )
,DA=DB=DC=2,过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则( )
A.MN的长度是定值 ![]()
B.MN长度的最小值是2
C.圆M面积的最小值是2π
D.圆M、N的面积和是定值8π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥P﹣ABCD中,AB=2,PA= ![]() ,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.
,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点. 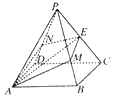
(1)若PM= ![]() PB,PN=λPD,求λ的值;
PB,PN=λPD,求λ的值;
(2)求直线PA与平面AMEN所成角的正弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=f( ![]() ),当x∈[1,4]时,f(x)=lnx,若在区间x∈[
),当x∈[1,4]时,f(x)=lnx,若在区间x∈[ ![]() ,4]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 .
,4]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点.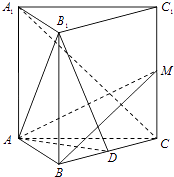
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且与直线
,1),且与直线 ![]() x+2y﹣4=0相切.
x+2y﹣4=0相切.
(1)求椭圆E的方程;
(2)若椭圆E与x轴交于M、N两点,椭圆E内部的动点P使|PM|、|PO|、|PN|成等比数列,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( ) 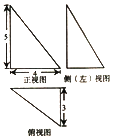
A.200π
B.50π
C.100π
D.![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com