
【题目】已知椭圆C:![]() 1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2
1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由向量的关系可得线段的关系,设|F2A|=3x,则|F2B|=2x,由椭圆的定义可得|F1A|=2a﹣3x,|F1B|=2a﹣2x,再由∠AF1B=90°,由勾股定理可得x的值,进而求出|AF1|,|AB|的值,进而求出∠F1AB的余弦值,由半角公式求出sin![]() ,进而求出离心率.
,进而求出离心率.
如图所示:
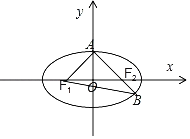
因为2![]() ,
,
设|F2A|=3x,|F2B|=2x,|
所以F1A|=2a﹣3x,|F1B|=2a﹣2x,
因为∠AF1B=90°,
所以(5x)2=(2a﹣3x)2+(2a﹣2x)2,
解得![]() ,
,
则|F2A|=a,|AB|![]() ,|F1B|
,|F1B|![]() a,|F1A|=a,
a,|F1A|=a,
所以可得A为短轴的顶点,
在△ABF1中,cos∠F1AB![]() ,
,
所以![]() sin
sin![]() ,
,
则![]() .
.
故选:B.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 若平面
若平面![]() ⊥平面
⊥平面![]()
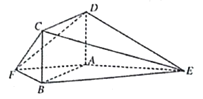
(Ⅰ)证明:平面![]() 平面ADF
平面ADF
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面![]() 若存在,求出此时三棱锥G一ABE与三棱锥
若存在,求出此时三棱锥G一ABE与三棱锥![]() 的体积之比,若不存在,请说明理由.
的体积之比,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国政府对PM2.5采用如下标准:

某市环保局从180天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
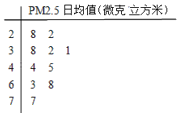
(1)求这10天数据的中位数.
(2)从这10天的数据中任取3天的数据,记![]() 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这10天的PM2.5日均值来估计这180天的空气质量情况,记![]() 为这180天空气质量达到一级的天数,求
为这180天空气质量达到一级的天数,求![]() 的均值.
的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上的点
上的点![]() 到焦点的距离为
到焦点的距离为![]() .
.

(1)求![]() 的值;
的值;
(2)如上图,已知动线段![]() (
(![]() 在
在![]() 的右边)在直线
的右边)在直线![]() 上,且
上,且![]() ,现过
,现过![]() 作
作![]() 的切线,取左边的切点
的切线,取左边的切点![]() ,过
,过![]() 作
作![]() 的切线,取右边的切点为
的切线,取右边的切点为![]() ,当
,当![]() ,求
,求![]() 点的横坐标
点的横坐标![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,__________,求△
,__________,求△![]() 的周长
的周长![]() 和面积
和面积![]() .
.
在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com