
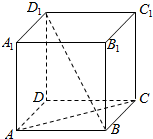
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$. 分析 连接BD,交AC于O点,取DD1的中点M,连接OM,求出△MAC的底面边长和高,代入三角形面积公式,可得答案.
解答 解:如下图所示: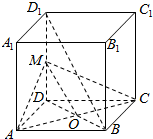
连接BD,交AC于O点,取DD1的中点M,连接OM,
则OM∥D1B,
由OM?平面MAC,D1B?平面MAC,
故此时平面MAC,即为过AC且与直线D1B平行的截面,
∵正方体ABCD-A1B1C1D1的棱长为2,
∴△MAC的底边长2$\sqrt{2}$,高OM=$\sqrt{{OD}^{2}+{DM}^{2}}$=$\sqrt{{\sqrt{2}}^{2}+{1}^{2}}$=$\sqrt{3}$,
故△MAC的面积S=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题考查的知识点是正方体的几何特征,线面平行的几何特征,三角形面积公式,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 过点(-1,0)的所有直线 | B. | 过点(1,0)的所有直线 | ||
| C. | 过点(1,0)且不垂直于x轴的所有直线 | D. | 过点(1,0)且除去x轴的所有直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
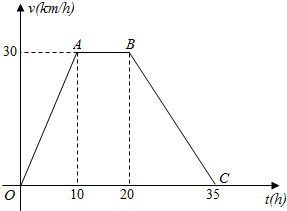 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (n-2)•2n | B. | 1-$\frac{1}{{2}^{n}}$ | C. | $\frac{2}{3}$(1-$\frac{1}{{4}^{n}}$) | D. | $\frac{2}{3}$(1-$\frac{1}{{2}^{n}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
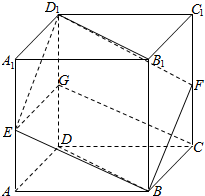 如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.
如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com