
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 经过椭圆C的左、右焦点
经过椭圆C的左、右焦点![]() ,
,![]() .
.
(1)求椭圆C的标准方程;
(2)若A,B,D,E是椭圆C上不同四点(其中点D在第一象限),且![]() ,直线
,直线![]() ,
,![]() 关于直线
关于直线![]() 对称,求直线
对称,求直线![]() 的方程.
的方程.
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】某疾病有甲、乙两种类型,对甲型患者的有效治疗只能通过注射药物Y,而乙型患者可以服药物A进行有效治疗,对该疾病患者可以通过药物A的临床检验确定甲型或乙型.检验的方法是:如果患者利用药物A完成第一个疗程有效,就可以确定是乙型;否则进行第二个疗程,如果完成第二个疗程有效,也可以确定是乙型,否则确定是甲型.为了掌握这种疾病患者中甲型、乙型所占比例,随机抽取100名患者作为样本通过药物A进行临床检验,检验结果是:样本中完成第二个疗程有效的患者是完成第一个疗程有效的患者的60%,且最终确定为甲型患者的有36人.
(1)根据检验结果,将频率视作概率,在利用药物A完成第一个疗程无效的患者中仼选3人,求其中甲型患者恰为2人的概率;
(2)该疾病的患者通过治疗,使血浆中某物质t的浓度降低到![]() 或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:
或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:![]() )的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数
)的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数![]() 和每个疗程后样本血浆中t的平均浓度
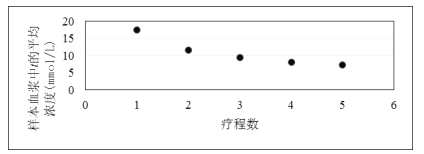
和每个疗程后样本血浆中t的平均浓度![]() 的数据作了初步处理,得到下面的散点图及一些统计量的值.
的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
3 | 11.0 | 0.46 | 262.5 | 30.1 | 55 | 1.458 |
/span>
上表中![]() ,
,![]() .
.
①根据散点图直接判断(不必说明理由),![]() 与
与![]() 哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
②患者在享受基本医疗保险及政府专项补助后,自己需承担的费用z(单位:元)与x,y的关系为![]() .在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
.在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为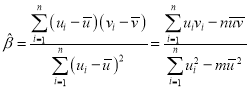 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x+1).
(1)若0<f(1-2x)-f(x)<1,求实数x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),当x∈[1,2]时,求函数y=g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.

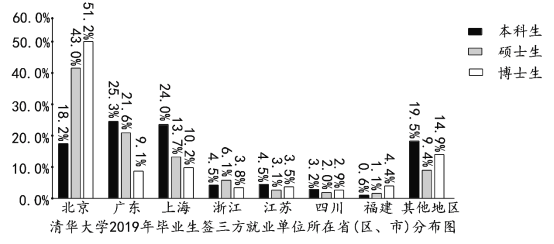
则下列选项错误的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com