
【题目】如图茎叶图表示的是甲,乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为 . 
【答案】![]()
【解析】解:由已知中的茎叶图可得 甲的5次综合测评中的成绩分别为88,89,90,91,92,
则甲的平均成绩: ![]() (88+89+90+91+92)=90
(88+89+90+91+92)=90
设污损数字为x
则乙的5次综合测评中的成绩分别为83,83,87,99,90+X
则乙的平均成绩: ![]() (83+83+87+99+90+x)=88.4+
(83+83+87+99+90+x)=88.4+ ![]() ,
,
当x=9,甲的平均数<乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为 ![]() ,
,
当x=8,甲的平均数=乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为 ![]() ,
,
甲的平均成绩超过乙的平均成绩的概率为1﹣ ![]() =
= ![]()
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解茎叶图(茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少),还要掌握平均数、中位数、众数(⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据)的相关知识才是答题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.

(1)当θ=![]() 时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;
时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;
(2)当θ=![]() 时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.
时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现阶段全国多地空气质量指数“爆表”.为探究车流量与![]() 浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到
浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到![]() 月某天
月某天![]() 个不同时段车流量与
个不同时段车流量与![]() 浓度的数据,如下表:
浓度的数据,如下表:
车流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)规定当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为优;当
,空气质量等级为优;当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程: ![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=![]() ,前n项和Sn满足Sn+1-Sn=(
,前n项和Sn满足Sn+1-Sn=(![]() )n+1(n∈N*).
)n+1(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天![]() 名读书者进行调查,将他们的年龄分成6段:
名读书者进行调查,将他们的年龄分成6段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
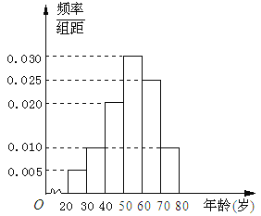
,![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:
(1)估计在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() . 问:是否存在正数m,使得对于任意正数
. 问:是否存在正数m,使得对于任意正数![]() ,可使
,可使![]() 为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com