
【题目】如图,![]() ,
,![]() ,
,![]() 是同一平面内的三条平行直线,
是同一平面内的三条平行直线, ![]() 与
与![]() 之间的距离是1,
之间的距离是1,![]() 与
与![]() 之间的距离是2,三角形
之间的距离是2,三角形![]() 的三个顶点分别在
的三个顶点分别在![]() ,
,![]() ,
,![]() 上.
上.
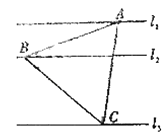
(1)若![]() 为正三角形,求其边长;
为正三角形,求其边长;
(2)若![]() 是以B为直角顶点的直角三角形,求其面积的最小值.
是以B为直角顶点的直角三角形,求其面积的最小值.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学中仅有一人申请了北京大学的自主招生考试,当他们被问到谁申请了北京大学的自主招生考试时,甲说:“丙或丁申请了”;乙说:“丙申请了”;丙说:“甲和丁都没有申请”;丁说:“乙申请了”,如果这四位同学中只有两人说的是对的,那么申请了北京大学的自主招生考试的同学是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入)
问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)设数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 满足:
满足:![]() ,且数列
,且数列![]() 的前
的前
n项和为![]() .
.
(1) 求![]() 的值;
的值;
(2) 求证:数列![]() 是等比数列;
是等比数列;
(3) 抽去数列![]() 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列![]() ,若
,若![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 的距离,等于它到直线
的距离,等于它到直线![]() 的距离.
的距离.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .
.
设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )且函数
)且函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)是否存在这样的实数![]() ,使
,使![]() 对所有的
对所有的![]() 均成立?若存在,求出适合条件的实数
均成立?若存在,求出适合条件的实数![]() 的值或范围;若不存在,说明理由.
的值或范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com