
【题目】已知函数![]() .
.
(1)用“五点法”在如图所示的虚线方框内作出函数![]() 在一个周期内的简图(要求:列表与描点,建立直角坐标系);
在一个周期内的简图(要求:列表与描点,建立直角坐标系);

(2)函数![]() 的图像可以通过函数
的图像可以通过函数![]() 的图像经过“先伸缩后平移”的规则变换而得到,请写出一个这样的变换!
的图像经过“先伸缩后平移”的规则变换而得到,请写出一个这样的变换!
【答案】(1)见解析;(2) g(x)=2cosx=2sin(x+![]() ),先横坐标伸长为原来的2倍,得到y=2sin(
),先横坐标伸长为原来的2倍,得到y=2sin(![]() +
+![]() ),再向右平移
),再向右平移![]() 个单位,得到 f(x)= 2sin(
个单位,得到 f(x)= 2sin(![]() x+
x+![]() )
)
o
【解析】试题分析:(1)根据已知中函数的解析式,描出函数图象上几个关键点的坐标,进而可得函数在一个周期上的草图;
(2) g(x)=2cosx=2sin(x+![]() ),先横坐标伸长为原来的2倍,得到y=2sin(
),先横坐标伸长为原来的2倍,得到y=2sin(![]() +
+![]() ),再向右平移
),再向右平移![]() 个单位即可.
个单位即可.
试题解析:
(1)
x | - | ||||
| 0 | π | 2π | ||
y | 0 | 2 | 0 | -2 | 0 |

(2) g(x)=2cosx=2sin(x+![]() ),先横坐标伸长为原来的2倍,得到y=2sin(
),先横坐标伸长为原来的2倍,得到y=2sin(![]() +
+![]() ),再向右平移
),再向右平移![]() 个单位(答案不唯一),得到 f(x)= 2sin(
个单位(答案不唯一),得到 f(x)= 2sin(![]() x+
x+![]() )
)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面四个结论中错误的是( )

A. 平面![]() 平面ABCD
平面ABCD
B. 直线BE,CF相交于一点
C. EF//平面BGD
D. ![]() 平面BGD
平面BGD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数,
是奇函数, ![]() 是偶函数.
是偶函数.
(1)求![]() 和
和![]() 的值;
的值;
(2)说明函数![]() 的单调性;若对任意的
的单调性;若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面ABC,底面三角形ABC是正三角形,E是BC中点,则下列叙述正确的是( )

A. AC⊥平面ABB1A1 B. CC1与B1E是异面直线
C. A1C1∥B1E D. AE⊥BB1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( ) 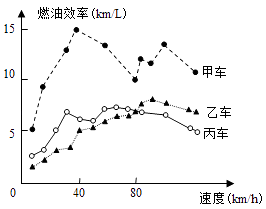
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为:
的方程为: ![]() 。
。
(1)求圆![]() 的圆心所在直线方程一般式;
的圆心所在直线方程一般式;
(2)若直线![]() 被圆
被圆![]() 截得弦长为
截得弦长为![]() ,试求实数
,试求实数![]() 的值;
的值;
(3)已知定点![]() ,且点
,且点![]() 是圆
是圆![]() 上两动点,当
上两动点,当![]() 可取得最大值为
可取得最大值为![]() 时,求满足条件的实数
时,求满足条件的实数![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com