
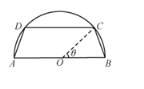
【题目】某景区拟将一半径为![]() 的半圆形绿地改建为等腰梯形
的半圆形绿地改建为等腰梯形![]() (如图,其中
(如图,其中![]() 为圆心,点
为圆心,点![]() 在半圆上)的放养观赏鱼的鱼池,周围四边建成观鱼长廊(宽度忽略不计).设
在半圆上)的放养观赏鱼的鱼池,周围四边建成观鱼长廊(宽度忽略不计).设![]() ,鱼池面积为
,鱼池面积为![]() (单位:
(单位:![]() ).
).
(1)求S关于![]() 的函数表达式,并求鱼池面积何时最大;
的函数表达式,并求鱼池面积何时最大;
(2)已知鱼池造价为每平方米2000元,长廊造价为每米3000元,问此次改建的最高造价不超过多少?(取![]() 计算)
计算)
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,(t为参数),曲线
,(t为参数),曲线![]() :
:![]() ,(
,(![]() 为参数).
为参数).
(1)以原点为极点,x轴正半轴为极轴建立极坐标系;当![]() 时,求
时,求![]() 与
与![]() 的交点的极坐标(其中极径
的交点的极坐标(其中极径![]() ,极角
,极角![]() );
);
(2)过坐标原点O作![]() 的垂线,垂足为A,P为OA中点,当
的垂线,垂足为A,P为OA中点,当![]() 变化时,求P点轨迹的参数方程,并指出它是什么曲线.
变化时,求P点轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率为![]() ,用随机模拟的方法估计这三天中恰有两天下雨的概率.可利用计算机产生0到9之间的整数值的随机数,如果我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,顺次产生的随机数如下:
,用随机模拟的方法估计这三天中恰有两天下雨的概率.可利用计算机产生0到9之间的整数值的随机数,如果我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,顺次产生的随机数如下:
90 79 66 19 19 25 27 19 32 81 24 58 56 96 83
43 12 57 39 30 27 55 64 88 73 01 13 13 79 89
,这三天中恰有两天下雨的概率约为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,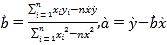 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年3月20日是国际幸福日,某电视台随机调查某一社区人们的幸福度.现从该社区群中随机抽取18名,用“10分制”记录了他们的幸福度指数,结果见如图所示茎叶图,其中以小数点前的一位数字为茎,小数点后的一位数字为叶.若幸福度不低于8.5分,则称该人的幸福度为“很幸福”.
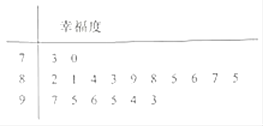
(Ⅰ)求从这18人中随机选取3人,至少有1人是“很幸福”的概率;
(Ⅱ)以这18人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“很幸福”的人数,求
表示抽到“很幸福”的人数,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
甲、乙、丙三名射击运动员射中目标的概率分别为![]()
![]() ,三人各射击一次,击中目标的次数记为
,三人各射击一次,击中目标的次数记为![]() .
.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (
(![]() =0,1,2,3)中, 若
=0,1,2,3)中, 若![]() 的值最大, 求实数
的值最大, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com