
【题目】某种植物感染![]() 病毒极易导致死亡,某生物研究所为此推出了一种抗
病毒极易导致死亡,某生物研究所为此推出了一种抗![]() 病毒的制剂,现对20株感染了
病毒的制剂,现对20株感染了![]() 病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成以下![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
吸收足量 | 吸收不足量 | 合计 | |
植株存活 | 1 | ||
植株死亡 | |||
合计 | 20 |
(2)①若在该样本“吸收不足量”的植株中随机抽取3株,记![]() 为“植株死亡”的数量,求
为“植株死亡”的数量,求![]() 得分布列和期望
得分布列和期望![]() ;
;
②将频率视为概率,现在对已知某块种植了1000株并感染了![]() 病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量
病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量![]() ,求
,求![]() .
.
参考数据: ,其中
,其中![]()
【答案】(1)不能在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关;(2)①分布列见解析,![]() ,②240
,②240
【解析】
(1)已知“植株存活”但“制剂吸收不足量”的植株共1株,由题意可得“植株存活”的13株,“植株死亡”的7株;“吸收足量”的15株,“吸收不足量”的5株,填表即可
(2)代入公式计算![]() ,有关(3)①样本中“制剂吸收不足量”有5株,其中“植株死亡”的有4株, 存活的1株,所以抽取的3株中
,有关(3)①样本中“制剂吸收不足量”有5株,其中“植株死亡”的有4株, 存活的1株,所以抽取的3株中![]() 的可能取值是2,3,根据古典概型计算即可. ②“植株存活”且“制剂吸收足量”的概率为
的可能取值是2,3,根据古典概型计算即可. ②“植株存活”且“制剂吸收足量”的概率为![]() ,
,![]()
解:(1) 由题意可得“植株存活”的13株,“植株死亡”的7株;“吸收足量”的15株,“吸收不足量”的5株,填写列联表如下:
吸收足量 | 吸收不足量 | 合计 | |
植株存活 | 12 | 1 | 13 |
植株死亡 | 3 | 4 | 7 |
合计 | 15 | 5 | 20 |
![]()
所以不能在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关.
①样本中“制剂吸收不足量”有5株,其中“植株死亡”的有4株, 存活的1株,
所以抽取的3株中![]() 的可能取值是2,/span>3.
的可能取值是2,/span>3.
其中![]() ,
, ![]()
![]() 的分布列为:
的分布列为:
| 2 | 3 |
|
|
|
所以![]() .
.
②![]()


科目:高中数学 来源: 题型:
【题目】已知三棱锥M-ABC中,MA=MB=MC=AC=![]() ,AB=BC=2,O为AC的中点,点N在边BC上,且
,AB=BC=2,O为AC的中点,点N在边BC上,且![]() .
.
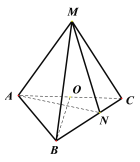
(1)证明:BO![]() 平面AMC;
平面AMC;
(2)求二面角N-AM-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用 (基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费
元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费![]() 基准保费
基准保费![]() (
(![]() 浮动比率
浮动比率![]() ).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:
).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:

某机构为了研究某一品牌普通6座以下私家车的投保情况,为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数,得到下面的柱状图:

已知小明家里有一辆该品牌普通6座以下私家车且需要续保,续保费用为![]() 元.
元.
(1)记![]() 为事件“
为事件“![]() ”,求
”,求![]() 的估计值;
的估计值;
(2)求![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() ,D为AB上一点,且
,D为AB上一点,且![]() 平面
平面![]() .
.
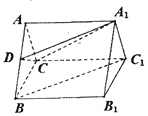
(1)求证:![]() ;
;
(2)若四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面ABC,直线
平面ABC,直线![]() 与平面ABC所成角的正切值等于2,
与平面ABC所成角的正切值等于2,![]() ,
,![]() ,求三楼柱
,求三楼柱![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长为a,b,c,有下列四个命题:
的三边长为a,b,c,有下列四个命题:
①以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
②以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
③以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
④以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在.
为边长的三角形一定存在.
其中正确的是( )
A.①③B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,使
,使![]() 是等边三角形且面积为
是等边三角形且面积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 与抛物线
与抛物线![]() 的一个交点,点
的一个交点,点![]() ,当
,当![]() 取得最小值时,求此时圆
取得最小值时,求此时圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,(其中
,(其中![]() 为自然对数的底数,
为自然对数的底数,![]() …).
…).
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)若![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com