
在正方形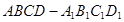 中,
中,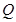 是
是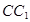 的中点,
的中点,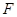 是侧面
是侧面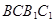 内的动点且
内的动点且 //平面
//平面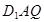 ,则
,则 与平面
与平面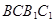 所成角的正切值得取值范围为 .
所成角的正切值得取值范围为 .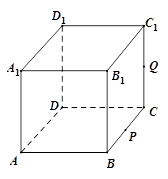
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:填空题
设m,n是两条不同的直线,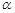 ,
,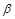 ,
, 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题:
①若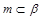 ,
,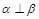 ,则
,则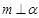 ;
;
②若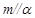 ,
,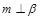 ,则
,则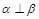 ;
;
③若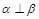 ,
,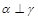 ,则
,则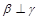 ;
;
④若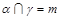 ,
,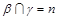 ,
,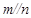 ,则
,则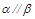 .
.
上面命题中,真命题的序号是 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=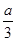 ,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.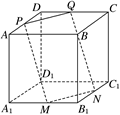
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对于直线m,n和平面α,β,γ,有如下四个命题:
①若m∥α,m⊥n,则n⊥α;
②若m⊥α,m⊥n,则n∥α;
③若α⊥β,γ⊥β,则α∥γ;
④若m⊥α,m∥n,n?β,则α⊥β.
其中正确命题的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com