【题目】棉花的纤维长度是棉花质量的重要指标．在一批棉花中抽测了60根棉花的纤维长度（单位：
），将样本数据制作成如下的频率分布直方图：
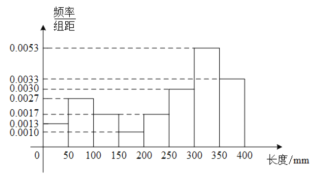
下列关于这批棉花质量状况的分析不正确的是（ ）
A.纤维长度在
的棉花的数量为9根
B.从这60根棉花中随机选取1根，其纤维长度在
的概率为0.335
C.有超过一半的棉花纤维长度能达到
以上
D.这批棉花的纤维长度的中位数的估计值为
.
科目：高中数学 来源： 题型：
【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系，对700棵高粱进行抽样调查，得到高度频数分布表如下：
表1：红粒高粱频数分布表
农作物高度（ |
|
|
|
|
|
|
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2：白粒高粱频数分布表
农作物高度（ |
|
|
|
|
|
|
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（1）估计这700棵高粱中红粒高粱的棵数；画出这700棵高粱中红粒高粱的频率分布直方图；
（2）①估计这700棵高粱中高粱高（cm）在
的概率；②在红粒高粱中，从高度（单位：cm）在
中任选3棵，设
表示所选3棵中高（单位：cm）在
的棵数，求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，
，动点
满足直线
与直线
的斜率之积为
，设点的轨迹为曲线
.
（1）求曲线的方程；
（2）若过点
的直线
与曲线交于
，
两点，过点
且与直线垂直的直线与
相交于点
，求
的最小值及此时直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，直线
的参数方程为
（
为参数），曲线
的参数方程为
（
为参数），以该直角坐标系的原点
为极点，
轴的非负半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（Ⅰ）分别求曲线的极坐标方程和曲线的直角坐标方程；
（Ⅱ）设直线交曲线于，
两点，交曲线于，
两点，求
的长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知王明比较喜爱打篮球，近来，他为了提高自己的投篮水平，制定了一个夏季训练计划.班主任为了了解其训练效果，开始训练前，统计了王明
场比赛的得分，计算出得分数据的中位数为
分，平均得分为
分，得分数据的方差为
，训练结束后统计了场比赛得分成绩茎叶图如下图：
（1）求王明训练结束后统计的场比赛得分的中位数，平均得分以及方差；
（2）若只从训练前后统计的各场比赛得分数据分析，训练计划对王明投篮水平的提高是否有帮助？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数u（x）＝xlnx，v（x）
x﹣1，m∈R．
（1）令m＝2，求函数h（x）
的单调区间；
（2）令f（x）＝u（x）﹣v（x），若函数f（x）恰有两个极值点x1，x2，且满足1
e（e为自然对数的底数）求x1x2的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
