
ΓΨΧβΡΩΓΩΡ≥œγ’ρœλ”ΠΓΑ¬ΧΥ°«ύ…ΫΨΆ «Ϋπ…Ϋ“χ…ΫΓ±ΒΡΚ≈’ΌΘ§“ρΒΊ÷Τ“ΥΒΡΫΪΗΟ’ρ¥ρ‘λ≥…ΓΑ…ζΧ§Υ°ΙϊΧΊ…Ϊ–Γ’ρΓ±Θ°Ψ≠Βς―–ΖΔœ÷ΘΚΡ≥’δœΓΥ°Ιϊ ςΒΡΒΞ÷ξ≤ζΝΩ![]() Θ®ΒΞΈΜΘΚ«ßΩΥΘ©”κ ©”ΟΖ Νœ
Θ®ΒΞΈΜΘΚ«ßΩΥΘ©”κ ©”ΟΖ Νœ![]() Θ®ΒΞΈΜΘΚ«ßΩΥΘ©¬ζΉψ»γœ¬ΙΊœΒΘΚ
Θ®ΒΞΈΜΘΚ«ßΩΥΘ©¬ζΉψ»γœ¬ΙΊœΒΘΚ Θ§Ζ Νœ≥…±ΨΆΕ»κΈΣ
Θ§Ζ Νœ≥…±ΨΆΕ»κΈΣ![]() ‘ΣΘ§ΤδΥϋ≥…±ΨΆΕ»κΘ®»γ≈ύ”ΐΙήάμΓΔ ©Ζ Β»»ΥΙΛΖ―Θ©
‘ΣΘ§ΤδΥϋ≥…±ΨΆΕ»κΘ®»γ≈ύ”ΐΙήάμΓΔ ©Ζ Β»»ΥΙΛΖ―Θ©![]() ‘ΣΘ°“―÷Σ’β÷÷Υ°ΙϊΒΡ –≥Γ έΦέ¥σ‘ΦΈΣ15‘ΣΘ·«ßΩΥΘ§«“œζ¬Ζ≥©Ά®Ι©≤Μ”Π«σΘ°Φ«ΗΟΥ°Ιϊ ςΒΡΒΞ÷ξάϊ»σΈΣ
‘ΣΘ°“―÷Σ’β÷÷Υ°ΙϊΒΡ –≥Γ έΦέ¥σ‘ΦΈΣ15‘ΣΘ·«ßΩΥΘ§«“œζ¬Ζ≥©Ά®Ι©≤Μ”Π«σΘ°Φ«ΗΟΥ°Ιϊ ςΒΡΒΞ÷ξάϊ»σΈΣ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©Θ°
Θ®ΒΞΈΜΘΚ‘ΣΘ©Θ°
Θ®ΔώΘ©«σ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®ΔρΘ©Β± ©”ΟΖ ΝœΈΣΕύ…Ό«ßΩΥ ±Θ§ΗΟΥ°Ιϊ ςΒΡΒΞ÷ξάϊ»σΉν¥σ?Ήν¥σάϊ»σ «Εύ…Ό?
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©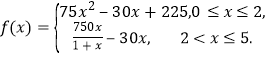 Θ®ΔρΘ©Β± ©”ΟΖ ΝœΈΣ4«ßΩΥ ±Θ§÷÷÷≤ΗΟΙϊ ςΜώΒΟΒΡΉν¥σάϊ»σ «480‘ΣΘ°
Θ®ΔρΘ©Β± ©”ΟΖ ΝœΈΣ4«ßΩΥ ±Θ§÷÷÷≤ΗΟΙϊ ςΜώΒΟΒΡΉν¥σάϊ»σ «480‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΩ…ΒΟfΘ®xΘ©ΘΫ15wΘ®xΘ©©¹30xΘ§‘ρΜ·ΈΣΖ÷ΕΈΚ· ΐΦ¥Ω…Θ§Θ®2Θ©ΗυΨίΖ÷ΕΈΚ· ΐΒΡΫβΈω ΫΦ¥Ω…«σ≥ωΉν¥σάϊ»σΘ°
Θ®ΔώΘ©”…“―÷Σ![]()
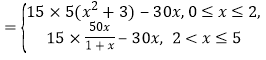
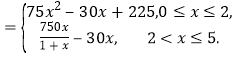
(Δρ)”…(Δώ)ΒΟ
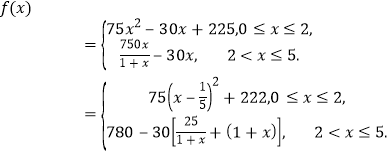
Β±![]() ±Θ§
±Θ§![]() ΘΜ
ΘΜ
Β±![]() ±Θ§
±Θ§![]()
![]()
Β±«“ΫωΒ±![]() ±Θ§Φ¥
±Θ§Φ¥![]() ±Β»Κ≈≥…ΝΔΘ°
±Β»Κ≈≥…ΝΔΘ°
“ρΈΣ![]() Θ§Υυ“‘Β±
Θ§Υυ“‘Β±![]() ±Θ§
±Θ§![]() Θ°
Θ°
ΓύΒ± ©”ΟΖ ΝœΈΣ4«ßΩΥ ±Θ§÷÷÷≤ΗΟΙϊ ςΜώΒΟΒΡΉν¥σάϊ»σ «480‘ΣΘ°


 ±ΩΧΉΦ±ΗΉ≈ νΦΌΉς“Β‘≠Ή”Ρή≥ωΑφ…γœΒΝ–¥πΑΗ
±ΩΧΉΦ±ΗΉ≈ νΦΌΉς“Β‘≠Ή”Ρή≥ωΑφ…γœΒΝ–¥πΑΗ νΦΌœΈΫ”ΫΧ≤ΡΤΎΡ© νΦΌ‘ΛœΑΈδΚΚ≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌœΈΫ”ΫΧ≤ΡΤΎΡ© νΦΌ‘ΛœΑΈδΚΚ≥ωΑφ…γœΒΝ–¥πΑΗ ΦΌΤΎΉς“Β νΦΌ≥…≥Λά÷‘Α–¬Ϋ°«ύ…ΌΡξ≥ωΑφ…γœΒΝ–¥πΑΗ
ΦΌΤΎΉς“Β νΦΌ≥…≥Λά÷‘Α–¬Ϋ°«ύ…ΌΡξ≥ωΑφ…γœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§«“¬ζΉψ
Θ§«“¬ζΉψ![]() .
.
Θ®IΘ©«σ÷ΛΘΚ![]() «Β»±» ΐΝ–ΘΜ
«Β»±» ΐΝ–ΘΜ
Θ®IIΘ©«σ÷ΛΘΚ![]() ≤Μ «Β»±» ΐΝ–.
≤Μ «Β»±» ΐΝ–.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫβΖ≈ΨϋΡ≥≤Ω‘Ύ Β±χ―ίΝΖΕ‘ΩΙ±»»ϋ÷–Θ§ΚλΓΔάΕΝΫΗω–ΓΉιΨυ≈…6»Υ≤ΈΦ” ΒΒ·…δΜςΘ§ΤδΥυΒΟ≥…Φ®ΒΡΨΞ“ΕΆΦ»γΆΦΥυ ΨΘ°
Θ®1Θ©ΗυΨί…δΜς ΐΨίΘ§ΦΤΥψΚλΓΔάΕΝΫΗω–ΓΉι…δΜς≥…Φ®ΒΡΨυ÷Β”κΖΫ≤νΘ§≤ΔΥΒΟςΚλΨϋΜΙ «άΕΨϋΒΡ≥…Φ®œύΕ‘±»ΫœΈ»Ε®ΘΜ
Θ®2Θ©»τ¥”άΕΨϋ6Οϊ Ω±χ÷–ΥφΜζ≥ι»ΓΝΫ»ΥΘ§«σΥυ≥ι»ΓΒΡΝΫ»ΥΒΡ≥…Φ®÷°≤ν≤Μ≥§Ιΐ2ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ß‘Ύ–ΘΨΆ≤ΆΒΡΗΏ“ΜΡξΦΕ―ß…ζ”–440ΟϊΘ§ΗΏΕΰΡξΦΕ―ß…ζ”–460ΟϊΘ§ΗΏ»ΐΡξΦΕ―ß…ζ”–500ΟϊΘΜΈΣΝΥΫβ―ß–Θ ≥ΧΟΒΡΖΰΈώ÷ ΝΩ«ιΩωΘ§”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”÷–≥ι»Γ70Οϊ―ß…ζΫχ––≥ι―υΒς≤ιΘ§Α――ß…ζΕ‘ ≥ΧΟΒΡΓΑΖΰΈώ¬ζ“βΕ»Γ±”κΓΑΦέΗώ¬ζ“βΕ»Γ±ΕΦΖ÷ΈΣΈεΗωΒ»ΦΕΘΚ1ΦΕΘ®Κή≤Μ¬ζ“βΘ©ΘΜ2ΦΕΘ®≤Μ¬ζ“βΘ©ΘΜ3ΦΕΘ®“ΜΑψΘ©ΘΜ4ΦΕΘ®¬ζ“βΘ©ΘΜ5ΦΕΘ®Κή¬ζ“βΘ©Θ§ΤδΆ≥ΦΤΫαΙϊ»γœ¬±μΘ®ΖΰΈώ¬ζ“βΕ»ΈΣxΘ§ΦέΗώ¬ζ“βΕ»ΈΣyΘ©Θ°
y | ΦέΗώ¬ζ“βΕ» | |||||
1 | 2 | 3 | 4 | 5 | ||
Ζΰ | 1 | 1 | 1 | 2 | 2 | 0 |
2 | 2 | 1 | 3 | 4 | 1 | |
3 | 3 | 7 | 8 | 8 | 4 | |
4 | 1 | 4 | 6 | 4 | 1 | |
5 | 0 | 1 | 2 | 3 | 1 | |
Θ®1Θ©«σΗΏΕΰΡξΦΕΙ≤≥ι»Γ―ß…ζ»Υ ΐΘΜ
Θ®2Θ©«σΓΑΖΰΈώ¬ζ“βΕ»Γ±ΈΣ3 ±ΒΡ5ΗωΓΑΦέΗώ¬ζ“βΕ»Γ± ΐΨίΒΡΖΫ≤νΘΜ
Θ®3Θ©ΈΣΧαΗΏ ≥ΧΟΖΰΈώ÷ ΝΩΘ§œ÷¥”xΘΦ3«“2ΓήyΘΦ4ΒΡΥυ”–―ß…ζ÷–ΥφΜζ≥ι»ΓΝΫ»Υ’ς«σ“βΦϊΘ§«σ÷Ν…Ό”–“Μ»ΥΒΡΓΑΖΰΈώ¬ζ“βΕ»Γ±ΈΣ1ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=x3©¹3axΘ®aΓ RΘ©
Θ®1Θ©Β±a=1 ±Θ§«σfΘ®xΘ©ΒΡΦΪ–Γ÷ΒΘΜ
Θ®2Θ©»τ÷±œΏx+y+m=0Ε‘»Έ“βΒΡmΓ RΕΦ≤Μ ««ζœΏy=fΘ®xΘ©ΒΡ«–œΏΘ§«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―χ’ΐ÷–―ß–¬–Θ«χΡΎ”–“ΜΩι“‘OΈΣ‘≤–ΡΘ§RΘ®ΒΞΈΜΘΚΟΉΘ©ΈΣΑκΨΕΒΡΑκ‘≤–ΈΜΡΒΊΘ®»γΆΦΘ©Θ§–ΘΉήΈώ¥ΠΦΤΜ°Ε‘ΤδΩΣΖΔάϊ”ΟΘ§Τδ÷–Ι≠–ΈBCD«χ”ρΘ®“θ”Α≤ΩΖ÷Θ©”Ο”Ύ÷÷÷≤Ιέ…Ά÷≤ΈοΘ§ΓςOBD«χ”ρ”Ο”Ύ÷÷÷≤Μ®Μή≥ω έΘ§Τδ”ύ«χ”ρ”Ο”Ύ÷÷÷≤≤ίΤΛ≥ω έΓΘ“―÷Σ÷÷÷≤Ιέ…Ά÷≤ΈοΒΡ≥…±Ψ «ΟΩΤΫΖΫΟΉ20‘ΣΘ§÷÷÷≤Μ®ΜήΒΡάϊ»σ «ΟΩΤΫΖΫΟΉ80‘ΣΘ§÷÷÷≤≤ίΤΛΒΡάϊ»σ «ΟΩΤΫΖΫΟΉ30‘ΣΓΘ
Θ®1Θ©…η![]() Θ®ΒΞΈΜΘΚΜΓΕ»Θ©Θ§”Ο
Θ®ΒΞΈΜΘΚΜΓΕ»Θ©Θ§”Ο![]() ±μ ΨΙ≠–ΈBCDΒΡΟφΜΐ
±μ ΨΙ≠–ΈBCDΒΡΟφΜΐ![]()
Θ®2Θ©»γΙϊΗΟ–ΘΉήΈώ¥Π―ϊ«κΡψΙφΜ°’βΩιΆΝΒΊΓΘ»γΚΈ…ηΦΤ![]() ΒΡ¥σ–Γ≤≈Ρή ΙΉήάϊ»σΉν¥σΘΩ≤Δ«σ≥ωΗΟΉν¥σ÷Β
ΒΡ¥σ–Γ≤≈Ρή ΙΉήάϊ»σΉν¥σΘΩ≤Δ«σ≥ωΗΟΉν¥σ÷Β

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§
Θ®ΔώΘ©»τ«ζœΏ![]() ‘Ύ
‘Ύ![]() ¥ΠΒΡΒΦ ΐΒ»”Ύ
¥ΠΒΡΒΦ ΐΒ»”Ύ![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡΦΪ÷ΒΘΜ
ΒΡΦΪ÷ΒΘΜ
Θ®ΔσΘ©Β±![]() ±Θ§
±Θ§![]() ‘Ύ
‘Ύ![]() …œΒΡΉν¥σ÷ΒΈΣ
…œΒΡΉν¥σ÷ΒΈΣ![]() Θ§«σ
Θ§«σ![]() ‘ΎΗΟ«χΦδ…œΒΡΉν–Γ÷Β
‘ΎΗΟ«χΦδ…œΒΡΉν–Γ÷Β
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
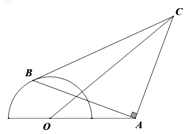
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ακ‘≤OΒΡ÷±ΨΕΈΣ2Θ§AΈΣ÷±ΨΕ―”≥ΛœΏ…œ“ΜΒψΘ§OA=2Θ§BΈΣΑκ‘≤…œ»Έ“β“ΜΒψΘ§“‘œΏΕΈABΈΣ―ϋΉςΒ»―ϋ÷±Ϋ«ΓςABCΘ®CΓΔOΝΫΒψ‘Ύ÷±œΏABΒΡΝΫ≤ύΘ©Θ§Β±ΓœAOB±δΜ· ±Θ§OCΓήmΚψ≥…ΝΔΘ§‘ρmΒΡΉν–Γ÷ΒΈΣ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ»±» ΐΝ–{an}ΒΡΗςœνΨυΈΣ’ΐ ΐΘ§«“a2=2,a4=![]() Θ°
Θ°
Θ®ΔώΘ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®ΔρΘ©…ηbn=log2an Θ§ «σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com