
【题目】两人约定在20∶00到21∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20∶00至21∶00各时刻相见的可能性是相等的,则他们两人在约定时间内相见的概率为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史。某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位; ![]() )数据,将数据分组如下表:
)数据,将数据分组如下表:
分组 | 频数 | 频率 |
| 4 | |
| 26 | |
| ||
| 28 | |
| 10 | |
| 2 | |
合计 | 100 |
(1)在答题卡上完成频率分布表;
(2)以表中的频率作为概率,估计重量落在![]() 中的概率及重量小于2.45的概率是多少?
中的概率及重量小于2.45的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知![]() 三人分配奖金的衰分比为
三人分配奖金的衰分比为![]() ,若
,若![]() 分得奖金1000元,则
分得奖金1000元,则![]() 所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
A.![]() ,12800元B.
,12800元B.![]() ,12800元
,12800元
C.![]() ,10240元D.
,10240元D.![]() ,10240元
,10240元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 内一定点
内一定点![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 内切.记动圆圆心
内切.记动圆圆心![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 方程;
方程;
(II)过点![]() 的动直线l交轨迹
的动直线l交轨迹![]() 于M,N两点,试问:在坐标平面上是否存在一个定点Q,使得以线段MN为直径的圆恒过点Q?若存在,求出点Q的坐标;若不存在,请说明理由.
于M,N两点,试问:在坐标平面上是否存在一个定点Q,使得以线段MN为直径的圆恒过点Q?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某桥是抛物线形拱桥,当水面在l时,拱顶离水面2 m,水面宽4 m.
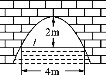
(1)水位下降1 m后,计算水面宽多少米?
(2)已知经过上述抛物线焦点且斜率为2的直线交抛物线于A、B两点,求A、B两点间的距离![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com