【题目】设函数
（1）当
时，求函数
在点
处的切线方程；
（2）若函数存在两个极值点
，
①求实数
的范围；
②证明：
.
【答案】（1）
；（2）
，证明详见解析．
【解析】
试题本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的极值和最值、利用导数求曲线的切线方程等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力．第一问，将
代入，对
求导，切点的纵坐标为
，斜率为
，利用点斜式写出切线方程；第二问，对求导，令
，将函数
存在两个极值点
，转化为方程
有两个不同的正根，利用二次函数的图象分析列出不等式，解出a的取值范围；对求导，求出的根，得到
的表达式，构造函数
，利用导数判断函数
的单调性，求出最小值，即证明了结论．
试题解析：（1）当a＝2时，
，
，
则
，
，所以切线方程为．4分
（2）
（
），令
，得
，
①函数
有两个极值点等价于方程有两个不同的正根，
设
，
所以
，
所以函数有两个极值点
，
，则，
②由，得，则
，
，
，
在区间
上递减，
，
所以
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】已知函数
.
(1)若
在
上单调递减，求
的取值范围；
(2)若在
处取得极值，判断当
时，存在几条切线与直线
平行，请说明理由；
(3)若有两个极值点
，求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两超市同时开业，第一年的全年销售额为a万元，由于经营方式不同，甲超市前n年的总销售额为
(n2－n＋2)万元，乙超市第n年的销售额比前一年销售额多a
万元．
(1)求甲、乙两超市第n年销售额的表达式；
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%，则该超市将被另一超市收购，判断哪一超市有可能被收购？如果有这种情况，将会出现在第几年？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在
）.
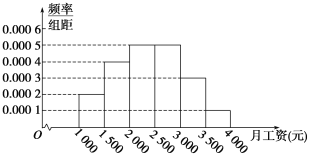
（1）求居民收入在
的频率；
（2）根据频率分布直方图算出样本数据的中位数；
（3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析，则月收入在
的这段应抽取多少人？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某区的区人大代表有教师6 人，分别来自甲、乙、丙、丁四个学校，其中甲校教师记为
，
，乙校教师记为
，
，丙校教师记为C，丁校教师记为D.现从这6 名教师代表中选出 3 名教师组成十九大报告宣讲团，要求甲、乙、丙、丁四个学校中，每校至多选出1名.
（1）请列出十九大报告宣讲团组成人员的全部可能结果；
（2）求教师被选中的概率；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，在点
处的切线方程为
.
（Ⅰ）求
的值；
（Ⅱ）已知
，当
时，
恒成立，求实数
的取值范围；
（Ⅲ）对于在
中的任意一个常数
，是否存在正数
，使得
，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市通过抽样调查的方法获得了100户居民某月用水量（单位：t）的频率分布直方图：
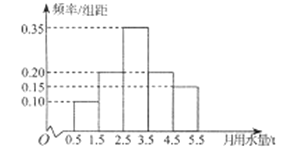
（Ⅰ）求这100户居民该月用水量的平均值；
（Ⅱ）从该月用水量在
和
两个区间的用户中，用分层抽样的方法邀请5户的户主共5人参加水价调整方案听证会，现从这5人中随机选取2人在会上进行陈述发言，求选取的2人均来自用水量低于2.5t的用户的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
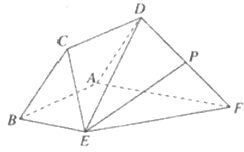
【题目】如图，已知菱形
与直角梯形
所在的平面互相垂直，其中
，
，
，
，
为
的中点
（Ⅰ）求证：
；
（Ⅱ）求二面角
的余弦值；
（Ⅲ）设
为线段
上一点，
，若直线
与平面所成角的正弦值为
，求
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
